Overlaps

export overlaps

What is overlaps?

The overlaps function checks if two geometries overlap. Two geometries can only overlap if they have the same dimension, and if they overlap, but one is not contained, within, or equal to the other.

Note that this means it is impossible for a single point to overlap with a single point and a line only overlaps with another line if only a section of each line is collinear.

To provide an example, consider these two lines:

import GeometryOps as GO
import GeoInterface as GI
using Makie
using CairoMakie

l1 = GI.LineString([(0.0, 0.0), (0.0, 10.0)])
l2 = GI.LineString([(0.0, -10.0), (0.0, 3.0)])
f, a, p = lines(GI.getpoint(l1), color = :blue)
scatter!(GI.getpoint(l1), color = :blue)
lines!(GI.getpoint(l2), color = :orange)
scatter!(GI.getpoint(l2), color = :orange)
f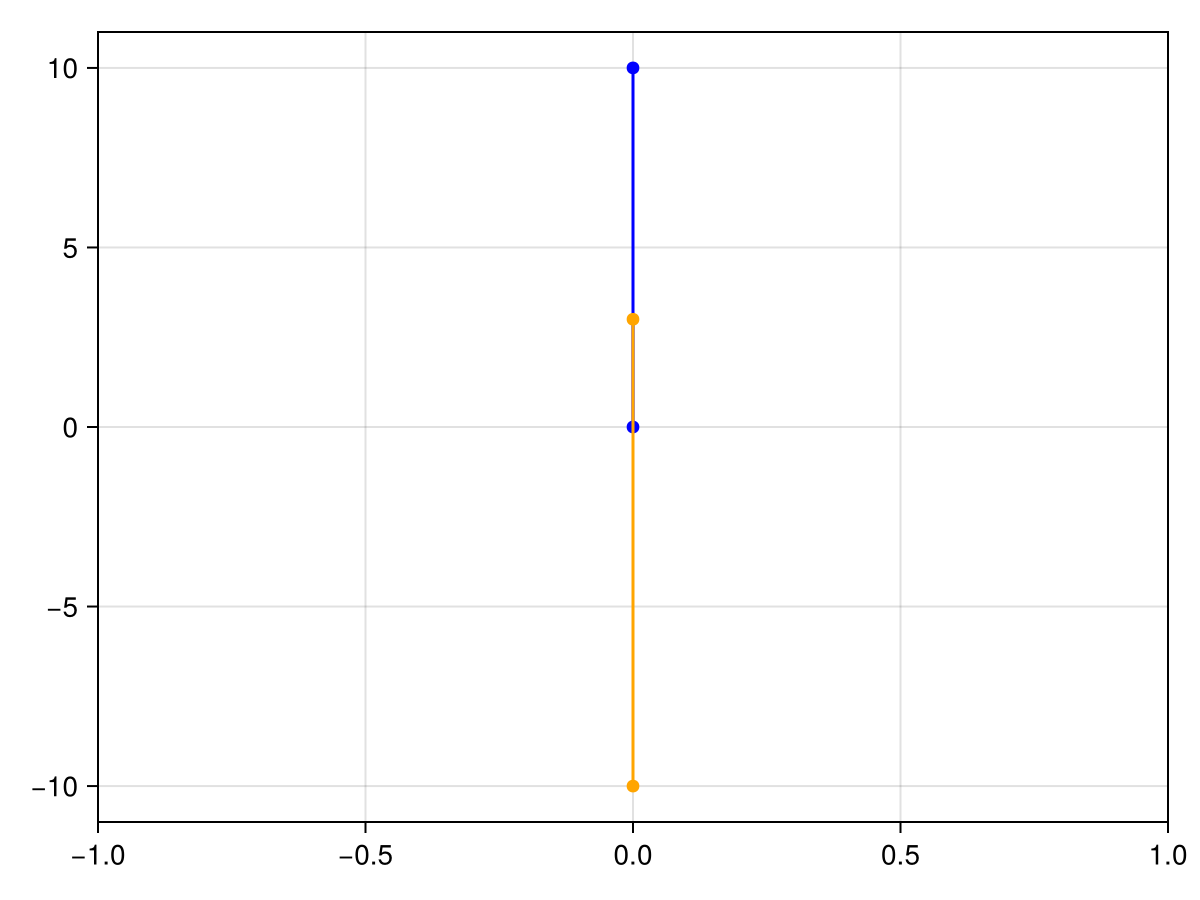

We can see that the two lines overlap in the plot:

GO.overlaps(l1, l2)  # true

true

Implementation

This is the GeoInterface-compatible implementation.

First, we implement a wrapper method that dispatches to the correct implementation based on the geometry trait. This is also used in the implementation, since it's a lot less work!

Note that that since only elements of the same dimension can overlap, any two geometries with traits that are of different dimensions automatically can return false.

For geometries with the same trait dimension, we must make sure that they share a point, an edge, or area for points, lines, and polygons/multipolygons respectively, without being contained.

"""
    overlaps(geom1, geom2)::Bool

Compare two Geometries of the same dimension and return true if their
intersection set results in a geometry different from both but of the same
dimension. This means one geometry cannot be within or contain the other and
they cannot be equal

# Examples
```jldoctest
import GeometryOps as GO, GeoInterface as GI
poly1 = GI.Polygon([[(0,0), (0,5), (5,5), (5,0), (0,0)]])
poly2 = GI.Polygon([[(1,1), (1,6), (6,6), (6,1), (1,1)]])

GO.overlaps(poly1, poly2)

output

true
```
"""
overlaps(geom1, geom2)::Bool = overlaps(
    GI.trait(geom1),
    geom1,
    GI.trait(geom2),
    geom2,
)

"""
    overlaps(::GI.AbstractTrait, geom1, ::GI.AbstractTrait, geom2)::Bool

For any non-specified pair, all have non-matching dimensions, return false.
"""
overlaps(::GI.AbstractTrait, geom1, ::GI.AbstractTrait, geom2) = false

"""
    overlaps(
        ::GI.MultiPointTrait, points1,
        ::GI.MultiPointTrait, points2,
    )::Bool

If the multipoints overlap, meaning some, but not all, of the points within the
multipoints are shared, return true.
"""
function overlaps(
    ::GI.MultiPointTrait, points1,
    ::GI.MultiPointTrait, points2,
)
    one_diff = false  # assume that all the points are the same
    one_same = false  # assume that all points are different
    for p1 in GI.getpoint(points1)
        match_point = false
        for p2 in GI.getpoint(points2)
            if equals(p1, p2)  # Point is shared
                one_same = true
                match_point = true
                break
            end
        end
        one_diff |= !match_point  # Point isn't shared
        one_same && one_diff && return true
    end
    return false
end

"""
    overlaps(::GI.LineTrait, line1, ::GI.LineTrait, line)::Bool

If the lines overlap, meaning that they are collinear but each have one endpoint
outside of the other line, return true. Else false.
"""
overlaps(::GI.LineTrait, line1, ::GI.LineTrait, line) =
    _overlaps((a1, a2), (b1, b2))

"""
    overlaps(
        ::Union{GI.LineStringTrait, GI.LinearRing}, line1,
        ::Union{GI.LineStringTrait, GI.LinearRing}, line2,
    )::Bool

If the curves overlap, meaning that at least one edge of each curve overlaps,
return true. Else false.
"""
function overlaps(
    ::Union{GI.LineStringTrait, GI.LinearRing}, line1,
    ::Union{GI.LineStringTrait, GI.LinearRing}, line2,
)
    edges_a, edges_b = map(sort! ∘ to_edges, (line1, line2))
    for edge_a in edges_a
        for edge_b in edges_b
            _overlaps(edge_a, edge_b) && return true
        end
    end
    return false
end

"""
    overlaps(
        trait_a::GI.PolygonTrait, poly_a,
        trait_b::GI.PolygonTrait, poly_b,
    )::Bool

If the two polygons intersect with one another, but are not equal, return true.
Else false.
"""
function overlaps(
    trait_a::GI.PolygonTrait, poly_a,
    trait_b::GI.PolygonTrait, poly_b,
)
    edges_a, edges_b = map(sort! ∘ to_edges, (poly_a, poly_b))
    return _line_intersects(edges_a, edges_b) &&
        !equals(trait_a, poly_a, trait_b, poly_b)
end

"""
    overlaps(
        ::GI.PolygonTrait, poly1,
        ::GI.MultiPolygonTrait, polys2,
    )::Bool

Return true if polygon overlaps with at least one of the polygons within the
multipolygon. Else false.
"""
function overlaps(
    ::GI.PolygonTrait, poly1,
    ::GI.MultiPolygonTrait, polys2,
)
    for poly2 in GI.getgeom(polys2)
        overlaps(poly1, poly2) && return true
    end
    return false
end

"""
    overlaps(
        ::GI.MultiPolygonTrait, polys1,
        ::GI.PolygonTrait, poly2,
    )::Bool

Return true if polygon overlaps with at least one of the polygons within the
multipolygon. Else false.
"""
overlaps(trait1::GI.MultiPolygonTrait, polys1, trait2::GI.PolygonTrait, poly2) =
    overlaps(trait2, poly2, trait1, polys1)

"""
    overlaps(
        ::GI.MultiPolygonTrait, polys1,
        ::GI.MultiPolygonTrait, polys2,
    )::Bool

Return true if at least one pair of polygons from multipolygons overlap. Else
false.
"""
function overlaps(
    ::GI.MultiPolygonTrait, polys1,
    ::GI.MultiPolygonTrait, polys2,
)
    for poly1 in GI.getgeom(polys1)
        overlaps(poly1, polys2) && return true
    end
    return false
end

#= If the edges overlap, meaning that they are collinear but each have one endpoint
outside of the other edge, return true. Else false. =#
function _overlaps(
    (a1, a2)::Edge,
    (b1, b2)::Edge,
    exact = _False(),
)

meets in more than one point

    seg_val, _, _ = _intersection_point(Float64, (a1, a2), (b1, b2); exact)

one end point is outside of other segment

    a_fully_within = _point_on_seg(a1, b1, b2) && _point_on_seg(a2, b1, b2)
    b_fully_within = _point_on_seg(b1, a1, a2) && _point_on_seg(b2, a1, a2)
    return seg_val == line_over && (!a_fully_within && !b_fully_within)
end

#= TODO: Once overlaps is swapped over to use the geom relations workflow, can
delete these helpers. =#

Checks if point is on a segment

function _point_on_seg(point, start, stop)

Parse out points

    x, y = GI.x(point), GI.y(point)
    x1, y1 = GI.x(start), GI.y(start)
    x2, y2 = GI.x(stop), GI.y(stop)
    Δxl = x2 - x1
    Δyl = y2 - y1

Determine if point is on segment

    cross = (x - x1) * Δyl - (y - y1) * Δxl
    if cross == 0  # point is on line extending to infinity

is line between endpoints

        if abs(Δxl) >= abs(Δyl)  # is line between endpoints
            return Δxl > 0 ? x1 <= x <= x2 : x2 <= x <= x1
        else
            return Δyl > 0 ? y1 <= y <= y2 : y2 <= y <= y1
        end
    end
    return false
end

#= Returns true if there is at least one intersection between edges within the
two lists of edges. =#
function _line_intersects(
    edges_a::Vector{<:Edge},
    edges_b::Vector{<:Edge};
)

Extents.intersects(to_extent(edges_a), to_extent(edges_b)) || return false

    for edge_a in edges_a
        for edge_b in edges_b
            _line_intersects(edge_a, edge_b) && return true
        end
    end
    return false
end

Returns true if there is at least one intersection between two edges.

function _line_intersects(edge_a::Edge, edge_b::Edge)
    seg_val, _, _ = _intersection_point(Float64, edge_a, edge_b; exact = _False())
    return seg_val != line_out
end

---

This page was generated using Literate.jl.