export coverage

What is coverage?

Coverage is the amount of geometry area within a bounding box defined by the minimum and maximum x and y-coordinates of that bounding box, or an Extent containing that information.

To provide an example, consider this rectangle:

import GeometryOps as GO
import GeoInterface as GI
using Makie
using CairoMakie

rect = GI.Polygon([[(-1,0), (-1,1), (1,1), (1,0), (-1,0)]])
cell = GI.Polygon([[(0, 0), (0, 2), (2, 2), (2, 0), (0, 0)]])
xmin, xmax, ymin, ymax = 0, 2, 0, 2
f, a, p = poly(collect(GI.getpoint(cell)); axis = (; aspect = DataAspect()))
poly!(collect(GI.getpoint(rect)))
f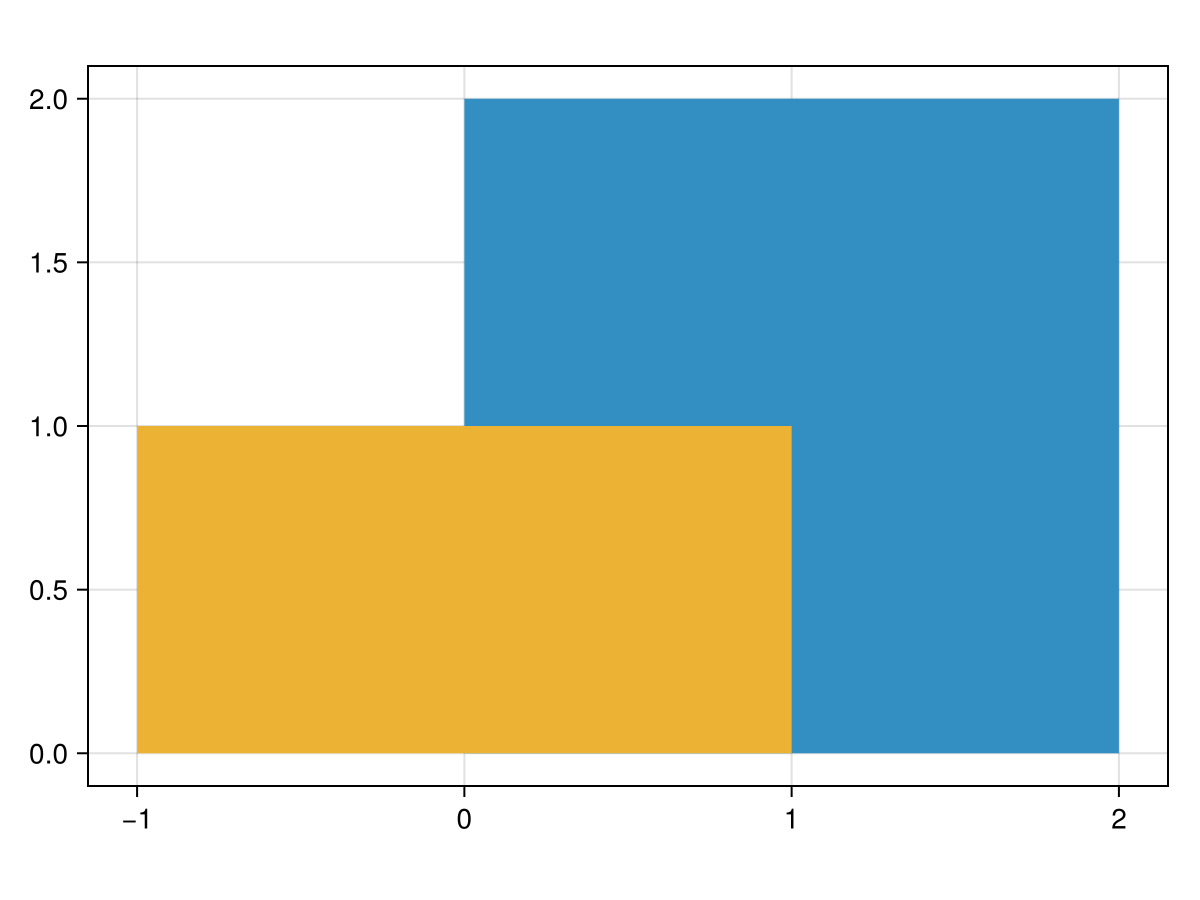

It is clear that half of the polygon is within the cell, so the coverage should be 1.0, half of the area of the rectangle.

GO.coverage(rect, xmin, xmax, ymin, ymax)

1.0

Implementation

This is the GeoInterface-compatible implementation. First, we implement a wrapper method that dispatches to the correct implementation based on the geometry trait. This is also used in the implementation, since it's a lot less work!

Note that the coverage is zero for all points and curves, even if the curves are closed like with a linear ring.

Targets for applys functions

const _COVERAGE_TARGETS = TraitTarget{Union{GI.PolygonTrait,GI.AbstractCurveTrait,GI.MultiPointTrait,GI.PointTrait}}()

Wall types for coverage

const UNKNOWN, NORTH, EAST, SOUTH, WEST = 0:4

"""
    coverage(geom, xmin, xmax, ymin, ymax, [T = Float64])::T

Returns the area of intersection between given geometry and grid cell defined by its minimum
and maximum x and y-values. This is computed differently for different geometries:

- The signed area of a point is always zero.
- The signed area of a curve is always zero.
- The signed area of a polygon is calculated by tracing along its edges and switching to the
    cell edges if needed.
- The coverage of a geometry collection, multi-geometry, feature collection of
    array/iterable is the sum of the coverages of all of the sub-geometries.

Result will be of type T, where T is an optional argument with a default value
of Float64.
"""
function coverage(geom, xmin, xmax, ymin, ymax,::Type{T} = Float64; threaded=false) where T <: AbstractFloat
    applyreduce(+, _COVERAGE_TARGETS, geom; threaded, init=zero(T)) do g
        _coverage(T, GI.trait(g), g, T(xmin), T(xmax), T(ymin), T(ymax))
    end
end

function coverage(geom, cell_ext::Extents.Extent, ::Type{T} = Float64; threaded=false) where T <: AbstractFloat
    (xmin, xmax), (ymin, ymax) = values(cell_ext)
    return coverage(geom, xmin, xmax, ymin, ymax, T; threaded = threaded)
end

Points, MultiPoints, Curves, MultiCurves

_coverage(::Type{T}, ::GI.AbstractGeometryTrait, geom, xmin, xmax, ymin, ymax; kwargs...) where T = zero(T)

Polygons

function _coverage(::Type{T}, ::GI.PolygonTrait, poly, xmin, xmax, ymin, ymax; exact = _False()) where T
    GI.isempty(poly) && return zero(T)
    cov_area = _coverage(T, GI.getexterior(poly), xmin, xmax, ymin, ymax; exact)
    cov_area == 0 && return cov_area

Remove hole coverage from total

    for hole in GI.gethole(poly)
        cov_area -= _coverage(T, hole, xmin, xmax, ymin, ymax; exact)
    end
    return cov_area
end

#= Calculates the area of the filled ring within the cell defined by corners with (xmin, ymin),
(xmin, ymax), (xmax, ymax), and (xmax, ymin). =#
function _coverage(::Type{T}, ring, xmin, xmax, ymin, ymax; exact) where T
    cov_area = zero(T)
    unmatched_out_wall, unmatched_out_point = UNKNOWN, (zero(T), zero(T))
    unmatched_in_wall, unmatched_in_point = unmatched_out_wall, unmatched_out_point

Loop over edges of polygon

    start_idx = 1
    for (i, p) in enumerate(GI.getpoint(ring))
        if !_point_in_cell(p, xmin, xmax, ymin, ymax)
            start_idx = i
            break
        end
    end
    ring_cw = isclockwise(ring)
    p1 = _tuple_point(GI.getpoint(ring, start_idx), T)

Must rotate clockwise for the algorithm to work

    point_idx = ring_cw ? Iterators.flatten((start_idx + 1:GI.npoint(ring), 1:start_idx)) :
        Iterators.flatten((start_idx - 1:-1:1, GI.npoint(ring):-1:start_idx))
    for i in point_idx
        p2 = _tuple_point(GI.getpoint(ring, i), T)

Determine if edge points are within the cell

        p1_in_cell = _point_in_cell(p1, xmin, xmax, ymin, ymax)
        p2_in_cell = _point_in_cell(p2, xmin, xmax, ymin, ymax)

If entire line segment is inside cell

        if p1_in_cell && p2_in_cell
            cov_area += _area_component(p1, p2)
            p1 = p2
            continue
        end

If edge passes outside of rectangle, determine which edge segments are added

        inter1, inter2 = _line_intersect_cell(T, p1, p2, xmin, xmax, ymin, ymax)

Endpoints of segment within the cell and wall they are on if known

        (start_wall, start_point), (end_wall, end_point) =
            if p1_in_cell
                ((UNKNOWN, p1), inter1)
            elseif p2_in_cell
                (inter1, (UNKNOWN, p2))
            else
                i1_to_p1 = _squared_euclid_distance(T, inter1[2], p1)
                i2_to_p1 = _squared_euclid_distance(T, inter2[2], p1)
                i1_to_p1 < i2_to_p1 ? (inter1, inter2) : (inter2, inter1)
            end

Add edge component

        cov_area += _area_component(start_point, end_point)

        if start_wall != UNKNOWN  # p1 out of cell
            if unmatched_out_wall == UNKNOWN
                unmatched_in_point = start_point
                unmatched_in_wall = start_wall
            else
                check_point = find_point_on_cell(unmatched_out_point, start_point,
                    unmatched_out_wall, start_wall,xmin, xmax, ymin, ymax)
                if _point_filled_curve_orientation(check_point, ring; in = true, on = false, out = false, exact)
                    cov_area += connect_edges(T, unmatched_out_point, start_point,
                        unmatched_out_wall, start_wall,xmin, xmax, ymin, ymax)
                else
                    cov_area += connect_edges(T, unmatched_out_point, unmatched_in_point,
                        unmatched_out_wall, unmatched_in_wall,xmin, xmax, ymin, ymax)
                    unmatched_out_wall == UNKNOWN
                end
            end
        end
        if end_wall != UNKNOWN  # p2 out of cell
            unmatched_out_wall, unmatched_out_point = end_wall, end_point
        end
        p1 = p2
    end

if unmatched in-point at beginning, close polygon with last out point

    if unmatched_in_wall != UNKNOWN
        cov_area += connect_edges(T, unmatched_out_point, unmatched_in_point,
            unmatched_out_wall, unmatched_in_wall,xmin, xmax, ymin, ymax)
    end
    cov_area = abs(cov_area) / 2

if grid cell is within polygon then the area is grid cell area

    if cov_area == 0
        if _point_filled_curve_orientation((xmin, ymin), ring; in = true, on = true, out = false, exact)
            cov_area = abs((xmax - xmin) * (ymax - ymin))
        end
    end
    return cov_area
end

Returns true of the given point is within the bounding box determined by x and y values

_point_in_cell(p, xmin, xmax, ymin, ymax) = xmin <= GI.x(p) <= xmax && ymin <= GI.y(p) <= ymax

Returns true if b is between a and c, exclusive of the maximum value, else false.

_between(b, a, c) = a ≤ b < c || c ≤ b < a

#= Determine intersections of the line from (x1, y1) to (x2, y2) with the bounding box
defined by the minimum and maximum x/y values. Since we are dealing with a single line
segment, we know that there is at maximum two intersection points.

For each intersection point that we find, return the wall that it passes through, as well as
the intersection point itself as a a tuple. If an intersection point isn't found, return the
wall as UNKNOWN and the point as a pair of zeros. =#
function _line_intersect_cell(::Type{T}, (x1, y1), (x2, y2), xmin, xmax, ymin, ymax) where T
    Δx, Δy = x2 - x1, y2 - y1
    inter1 = (UNKNOWN, (zero(T), zero(T)))
    inter2 = inter1
    if Δx == 0  # If line is vertical, only consider north and south
        if xmin ≤ x1 ≤ xmax
            inter1 = _between(ymax, y1, y2) ? (NORTH, (x1, ymax)) : inter1
            inter2 = _between(ymin, y1, y2) ? (SOUTH, (x1, ymin)) : inter2
        end
    elseif Δy == 0 # If line is horizontal, only consider east and west
        if ymin ≤ y1 ≤ ymax
            inter1 = _between(xmax, x1, x2) ? (EAST, (xmax, y1)) : inter1
            inter2 = _between(xmin, x1, x2) ? (WEST, (xmin, y1)) : inter2
        end
    else  # Line is tilted, must consider all edges, but only two can intersect
        m = Δy / Δx
        b = y1 - m * x1

Calculate and check potential intersections

        xn = (ymax - b) / m
        if xmin ≤ xn ≤ xmax && _between(xn, x1, x2) && _between(ymax, y1, y2)
            inter1 = (NORTH, (xn, ymax))
        end
        xs = (ymin - b) / m
        if xmin ≤ xs ≤ xmax && _between(xs, x1, x2) && _between(ymin, y1, y2)
            new_intr = (SOUTH, (xs, ymin))
            (inter1[1] == UNKNOWN) ? (inter1 = new_intr) : (inter2 = new_intr)
        end
        ye =  m * xmax + b
        if ymin ≤ ye ≤ ymax && _between(ye, y1, y2) && _between(xmax, x1, x2)
            new_intr = (EAST, (xmax, ye))
            (inter1[1] == UNKNOWN) ? (inter1 = new_intr) : (inter2 = new_intr)
        end
        yw = m * xmin + b
        if ymin ≤ yw ≤ ymax && _between(yw, y1, y2) && _between(xmin, x1, x2)
            new_intr = (WEST, (xmin, yw))
            (inter1[1] == UNKNOWN) ? (inter1 = new_intr) : (inter2 = new_intr)
        end
    end
    if inter1[1] == UNKNOWN  # first intersection must be known, if one exists
        inter1, inter2 = inter2, inter1
    end
    return inter1, inter2
end

Finds point of cell edge between p1 and p2 given which walls they are on

function find_point_on_cell(p1, p2, wall1, wall2, xmin, xmax, ymin, ymax)
    x1, y1 = p1
    x2, y2 = p2
    mid_point = if wall1 == wall2 && _is_clockwise_from(p1, p2, wall1)
        (x1 + x2) / 2, (y1 + y2) / 2
    elseif wall1 == NORTH
        (xmax, ymax)
    elseif wall1 == EAST
        (xmax, ymin)
    elseif wall1 == SOUTH
        (xmin, ymin)
    else
        (xmin, ymax)
    end
    return mid_point
end

#= Area component of shoelace formula coming from the distance between point 1 and point 2
along grid cell walls in between the two points. =#
function connect_edges(::Type{T}, p1, p2, wall1, wall2, xmin, xmax, ymin, ymax) where {T}
    connect_area = zero(T)
    if wall1 == wall2 && _is_clockwise_from(p1, p2, wall1)
        connect_area += _area_component(p1, p2)
    else

From the point to the corner of wall 1

        connect_area += _partial_edge_out_area(p1, xmin, xmax, ymin, ymax, wall1)

Any intermediate walls (full length)

        next_wall, last_wall = wall1 + 1, wall2 - 1
        if wall2 > wall1
            for wall in next_wall:last_wall
                connect_area += _full_edge_area(xmin, xmax, ymin, ymax, wall)
            end
        else
            for wall in Iterators.flatten((next_wall:WEST, NORTH:last_wall))
                connect_area += _full_edge_area(xmin, xmax, ymin, ymax, wall)
            end
        end

From the corner of wall 2 to the point

        connect_area += _partial_edge_in_area(p2, xmin, xmax, ymin, ymax, wall2)
    end
    return connect_area
end

True if (x1, y1) is clockwise from (x2, y2) on the same wall

_is_clockwise_from((x1, y1), (x2, y2), wall) = (wall == NORTH && x2 > x1) ||
    (wall == EAST && y2 < y1) || (wall == SOUTH && x2 < x1) || (wall == WEST && y2 > y1)

#= Returns the area component of a full edge of the bounding box defined by the min and max
values and the wall. =#
_full_edge_area(xmin, xmax, ymin, ymax, wall) = if wall == NORTH
        ymax * (xmin - xmax)
    elseif wall == EAST
        xmax * (ymin - ymax)
    elseif wall == SOUTH
        ymin * (xmax - xmin)
    else
        xmin * (ymax - ymin)
    end

#= Returns the area component of part of one wall, from its "starting corner" (going
clockwise) to the point (x2, y2). =#
function _partial_edge_in_area((x2, y2), xmin, xmax, ymin, ymax, wall)
    x_wall = (wall == NORTH || wall == WEST) ? xmin : xmax
    y_wall = (wall == NORTH || wall == EAST) ? ymax : ymin
    return x_wall * y2 - x2 * y_wall
end

#= Returns the area component of part of one wall, from the point (x1, y1) to its
"ending corner" (going clockwise). =#
function _partial_edge_out_area((x1, y1), xmin, xmax, ymin, ymax, wall)
    x_wall = (wall == NORTH || wall == EAST) ? xmax : xmin
    y_wall = (wall == NORTH || wall == WEST) ? ymax : ymin
    return x1 * y_wall - x_wall * y1
end

---

This page was generated using Literate.jl.