Polygon cutting

export cut

What is cut?

The cut function cuts a polygon through a line segment. This is inspired by functions such as Matlab's cutpolygon function.

To provide an example, consider the following polygon and line:

import GeoInterface as GI, GeometryOps as GO
using CairoMakie
using Makie

poly = GI.Polygon([[(0.0, 0.0), (10.0, 0.0), (10.0, 10.0), (0.0, 10.0), (0.0, 0.0)]])
line = GI.Line([(5.0, -5.0), (5.0, 15.0)])
cut_polys = GO.cut(poly, line)

f, a, p1 = Makie.poly(collect(GI.getpoint(cut_polys[1])); color = (:blue, 0.5))
Makie.poly!(collect(GI.getpoint(cut_polys[2])); color = (:orange, 0.5))
Makie.lines!(GI.getpoint(line); color = :black)
f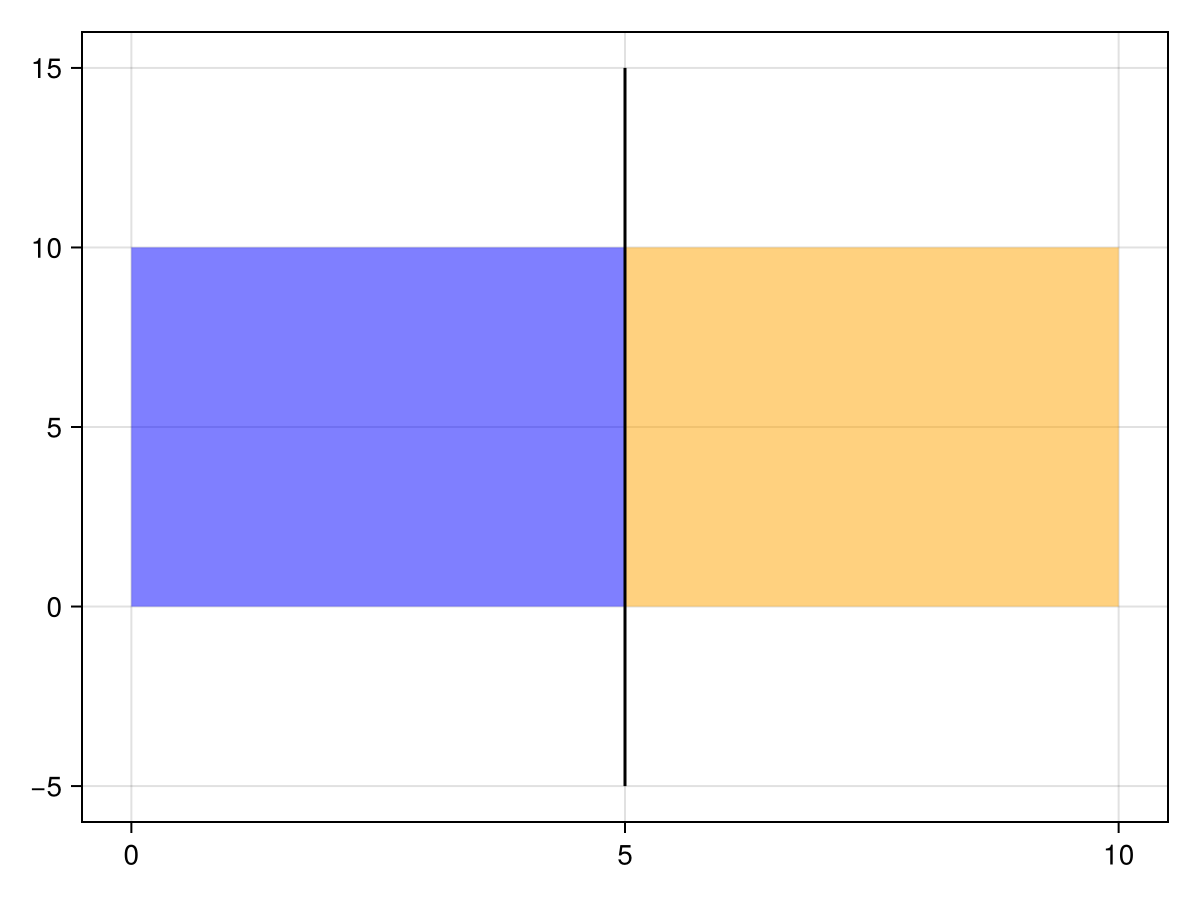

Implementation

This function depends on polygon clipping helper function and is inspired by the Greiner-Hormann clipping algorithm used elsewhere in this library. The inspiration came from this Stack Overflow discussion.

"""
    cut(geom, line, [T::Type])

Return given geom cut by given line as a list of geometries of the same type as the input
geom. Return the original geometry as only list element if none are found. Line must cut
fully through given geometry or the original geometry will be returned.

Note: This currently doesn't work for degenerate cases there line crosses through vertices.

# Example

```jldoctest
import GeoInterface as GI, GeometryOps as GO

poly = GI.Polygon([[(0.0, 0.0), (10.0, 0.0), (10.0, 10.0), (0.0, 10.0), (0.0, 0.0)]])
line = GI.Line([(5.0, -5.0), (5.0, 15.0)])
cut_polys = GO.cut(poly, line)
GI.coordinates.(cut_polys)

output

2-element Vector{Vector{Vector{Vector{Float64}}}}:
 [[[0.0, 0.0], [5.0, 0.0], [5.0, 10.0], [0.0, 10.0], [0.0, 0.0]]]
 [[[5.0, 0.0], [10.0, 0.0], [10.0, 10.0], [5.0, 10.0], [5.0, 0.0]]]
```
"""
cut(geom, line, ::Type{T} = Float64) where {T <: AbstractFloat} =
    _cut(T, GI.trait(geom), geom, GI.trait(line), line; exact = _True())

#= Cut a given polygon by given line. Add polygon holes back into resulting pieces if there
are any holes. =#
function _cut(::Type{T}, ::GI.PolygonTrait, poly, ::GI.LineTrait, line; exact) where T
    ext_poly = GI.getexterior(poly)
    poly_list, intr_list = _build_a_list(T, ext_poly, line; exact)
    n_intr_pts = length(intr_list)

If an impossible number of intersection points, return original polygon

    if n_intr_pts < 2 || isodd(n_intr_pts)
        return [tuples(poly)]
    end

Cut polygon by line

    cut_coords = _cut(T, ext_poly, line, poly_list, intr_list, n_intr_pts; exact)

Close coords and create polygons

    for c in cut_coords
        push!(c, c[1])
    end
    cut_polys = [GI.Polygon([c]) for c in cut_coords]

Add original polygon holes back in

    remove_idx = falses(length(cut_polys))
    _add_holes_to_polys!(T, cut_polys, GI.gethole(poly), remove_idx; exact)
    return cut_polys
end

Many types aren't implemented

function _cut(::Type{T}, trait::GI.AbstractTrait, geom, line; kwargs...) where T
    @assert(
        false,
        "Cutting of $trait isn't implemented yet.",
    )
    return nothing
end

#= Cutting algorithm inspired by Greiner and Hormann clipping algorithm. Returns coordinates
of cut geometry in Vector{Vector{Tuple}} format.

Note: degenerate cases where intersection points are vertices do not work right now. =#
function _cut(::Type{T}, geom, line, geom_list, intr_list, n_intr_pts; exact) where T

Sort and categorize the intersection points

    sort!(intr_list, by = x -> geom_list[x].fracs[2])
    _flag_ent_exit!(GI.LineTrait(), line, geom_list; exact)

Add first point to output list

    return_coords = [[geom_list[1].point]]
    cross_backs = [(T(Inf),T(Inf))]
    poly_idx = 1
    n_polys = 1

Walk around original polygon to find split polygons

    for (pt_idx, curr) in enumerate(geom_list)
        if pt_idx > 1
            push!(return_coords[poly_idx], curr.point)
        end
        if curr.inter

Find cross back point for current polygon

            intr_idx = findfirst(x -> equals(curr.point, geom_list[x].point), intr_list)
            cross_idx = intr_idx + (curr.ent_exit ? 1 : -1)
            cross_idx = cross_idx < 1 ? n_intr_pts : cross_idx
            cross_idx = cross_idx > n_intr_pts ? 1 : cross_idx
            cross_backs[poly_idx] = geom_list[intr_list[cross_idx]].point

Check if current point is a cross back point

            next_poly_idx = findfirst(x -> equals(x, curr.point), cross_backs)
            if isnothing(next_poly_idx)
                push!(return_coords, [curr.point])
                push!(cross_backs, curr.point)
                n_polys += 1
                poly_idx = n_polys
            else
                push!(return_coords[next_poly_idx], curr.point)
                poly_idx = next_poly_idx
            end
        end
    end
    return return_coords
end

---

This page was generated using Literate.jl.