Area and signed area

export area, signed_area

What is area? What is signed area?

Area is the amount of space occupied by a two-dimensional figure. It is always a positive value. Signed area is simply the integral over the exterior path of a polygon, minus the sum of integrals over its interior holes. It is signed such that a clockwise path has a positive area, and a counterclockwise path has a negative area. The area is the absolute value of the signed area.

To provide an example, consider this rectangle:

import GeometryOps as GO
import GeoInterface as GI
using Makie
using CairoMakie

rect = GI.Polygon([[(0,0), (0,1), (1,1), (1,0), (0, 0)]])
f, a, p = poly(collect(GI.getpoint(rect)); axis = (; aspect = DataAspect()))

This is clearly a rectangle, etc. But now let's look at how the points look:

lines!(
    collect(GI.getpoint(rect));
    color = 1:GI.npoint(rect), linewidth = 10.0)
f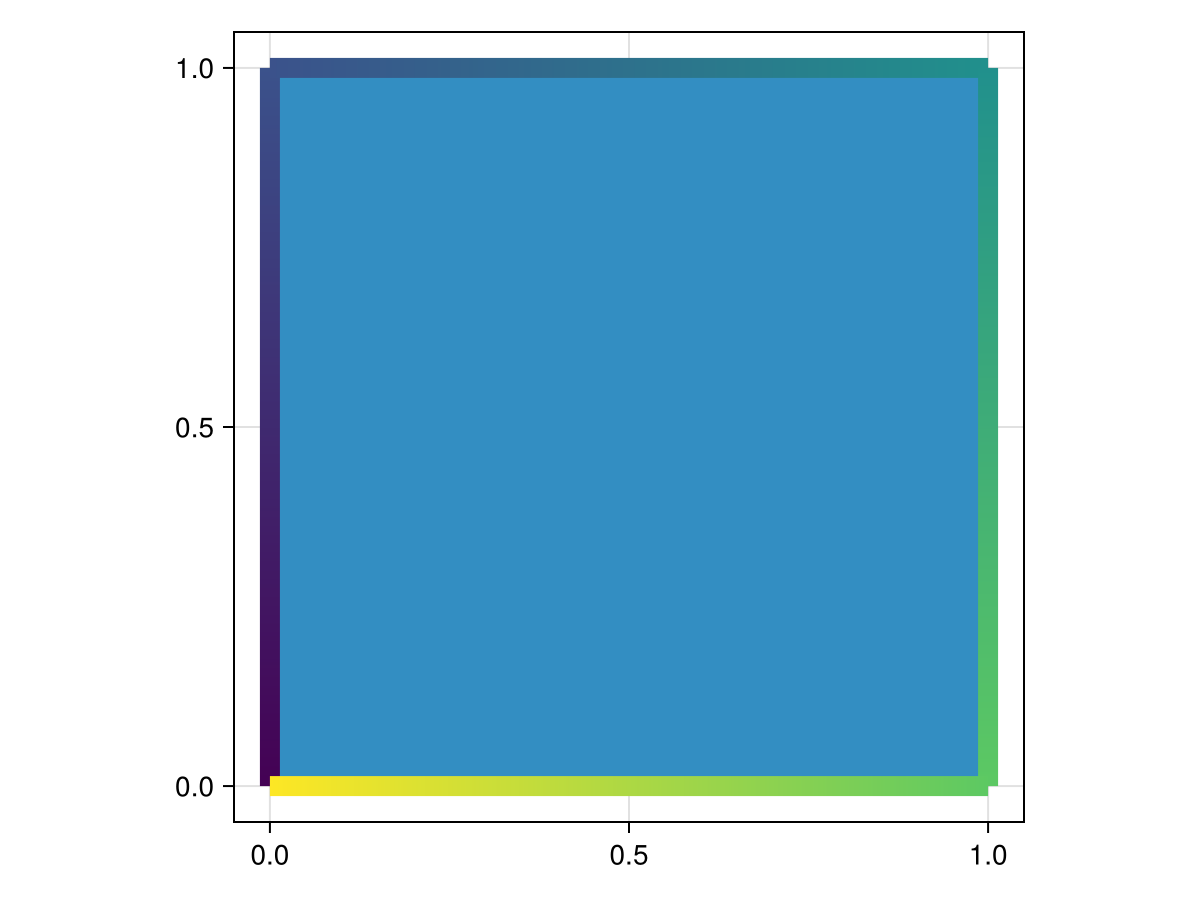

The points are ordered in a counterclockwise fashion, which means that the signed area is negative. If we reverse the order of the points, we get a positive area.

GO.signed_area(rect)  # -1.0

-1.0

Implementation

This is the GeoInterface-compatible implementation. First, we implement a wrapper method that dispatches to the correct implementation based on the geometry trait. This is also used in the implementation, since it's a lot less work!

Note that area and signed area are zero for all points and curves, even if the curves are closed like with a linear ring. Also note that signed area really only makes sense for polygons, given with a multipolygon can have several polygons each with a different orientation and thus the absolute value of the signed area might not be the area. This is why signed area is only implemented for polygons.

Targets for applys functions

const _AREA_TARGETS = TraitTarget{Union{GI.PolygonTrait,GI.AbstractCurveTrait,GI.MultiPointTrait,GI.PointTrait}}()

"""
    area(geom, [T = Float64])::T

Returns the area of a geometry or collection of geometries.
This is computed slightly differently for different geometries:

    - The area of a point/multipoint is always zero.
    - The area of a curve/multicurve is always zero.
    - The area of a polygon is the absolute value of the signed area.
    - The area multi-polygon is the sum of the areas of all of the sub-polygons.
    - The area of a geometry collection, feature collection of array/iterable
        is the sum of the areas of all of the sub-geometries.

Result will be of type T, where T is an optional argument with a default value
of Float64.
"""
function area(geom, ::Type{T} = Float64; threaded=false) where T <: AbstractFloat
    applyreduce(+, _AREA_TARGETS, geom; threaded, init=zero(T)) do g
        _area(T, GI.trait(g), g)
    end
end

"""
    signed_area(geom, [T = Float64])::T

Returns the signed area of a single geometry, based on winding order.
This is computed slightly differently for different geometries:

    - The signed area of a point is always zero.
    - The signed area of a curve is always zero.
    - The signed area of a polygon is computed with the shoelace formula and is
    positive if the polygon coordinates wind clockwise and negative if
    counterclockwise.
    - You cannot compute the signed area of a multipolygon as it doesn't have a
    meaning as each sub-polygon could have a different winding order.

Result will be of type T, where T is an optional argument with a default value
of Float64.
"""
signed_area(geom, ::Type{T} = Float64) where T <: AbstractFloat =
    _signed_area(T, GI.trait(geom), geom)

Points, MultiPoints, Curves, MultiCurves

_area(::Type{T}, ::GI.AbstractGeometryTrait, geom) where T = zero(T)

_signed_area(::Type{T}, ::GI.AbstractGeometryTrait, geom) where T = zero(T)

LibGEOS treats linear rings as zero area. I disagree with that but we should probably maintain compatibility...

_area(::Type{T}, tr::GI.LinearRingTrait, geom) where T = 0 # could be abs(_signed_area(T, tr, geom))

_signed_area(::Type{T}, ::GI.LinearRingTrait, geom) where T = 0 # could be _signed_area(T, tr, geom)

Polygons

_area(::Type{T}, trait::GI.PolygonTrait, poly) where T =
    abs(_signed_area(T, trait, poly))

function _signed_area(::Type{T}, ::GI.PolygonTrait, poly) where T
    GI.isempty(poly) && return zero(T)
    s_area = _signed_area(T, GI.getexterior(poly))
    area = abs(s_area)
    area == 0 && return area

Remove hole areas from total

    for hole in GI.gethole(poly)
        area -= abs(_signed_area(T, hole))
    end

Winding of exterior ring determines sign

    return area * sign(s_area)
end

One term of the shoelace area formula

_area_component(p1, p2) = GI.x(p1) * GI.y(p2) - GI.y(p1) * GI.x(p2)

#= Calculates the signed area of a given curve. This is equivalent to integrating
to find the area under the curve. Even if curve isn't explicitly closed by
repeating the first point at the end of the coordinates, curve is still assumed
to be closed. =#
function _signed_area(::Type{T}, geom) where T
    area = zero(T)
    np = GI.npoint(geom)
    np == 0 && return area

    first = true
    local pfirst, p1

Integrate the area under the curve

    for p2 in GI.getpoint(geom)

Skip the first and do it later This lets us work within one iteration over geom, which means on C call when using points from external libraries.

        if first
            p1 = pfirst = p2
            first = false
            continue
        end

Accumulate the area into area

        area += _area_component(p1, p2)
        p1 = p2
    end

Complete the last edge. If the first and last where the same this will be zero

    p2 = pfirst
    area += _area_component(p1, p2)
    return T(area / 2)
end

---

This page was generated using Literate.jl.