Centroid

export centroid, centroid_and_length, centroid_and_area

What is the centroid?

The centroid is the geometric center of a line string or area(s). Note that the centroid does not need to be inside of a concave area.

Further note that by convention a line, or linear ring, is calculated by weighting the line segments by their length, while polygons and multipolygon centroids are calculated by weighting edge's by their 'area components'.

To provide an example, consider this concave polygon in the shape of a 'C':

import GeometryOps as GO
import GeoInterface as GI
using Makie
using CairoMakie

cshape = GI.Polygon([[(0,0), (0,3), (3,3), (3,2), (1,2), (1,1), (3,1), (3,0), (0,0)]])
f, a, p = poly(collect(GI.getpoint(cshape)); axis = (; aspect = DataAspect()))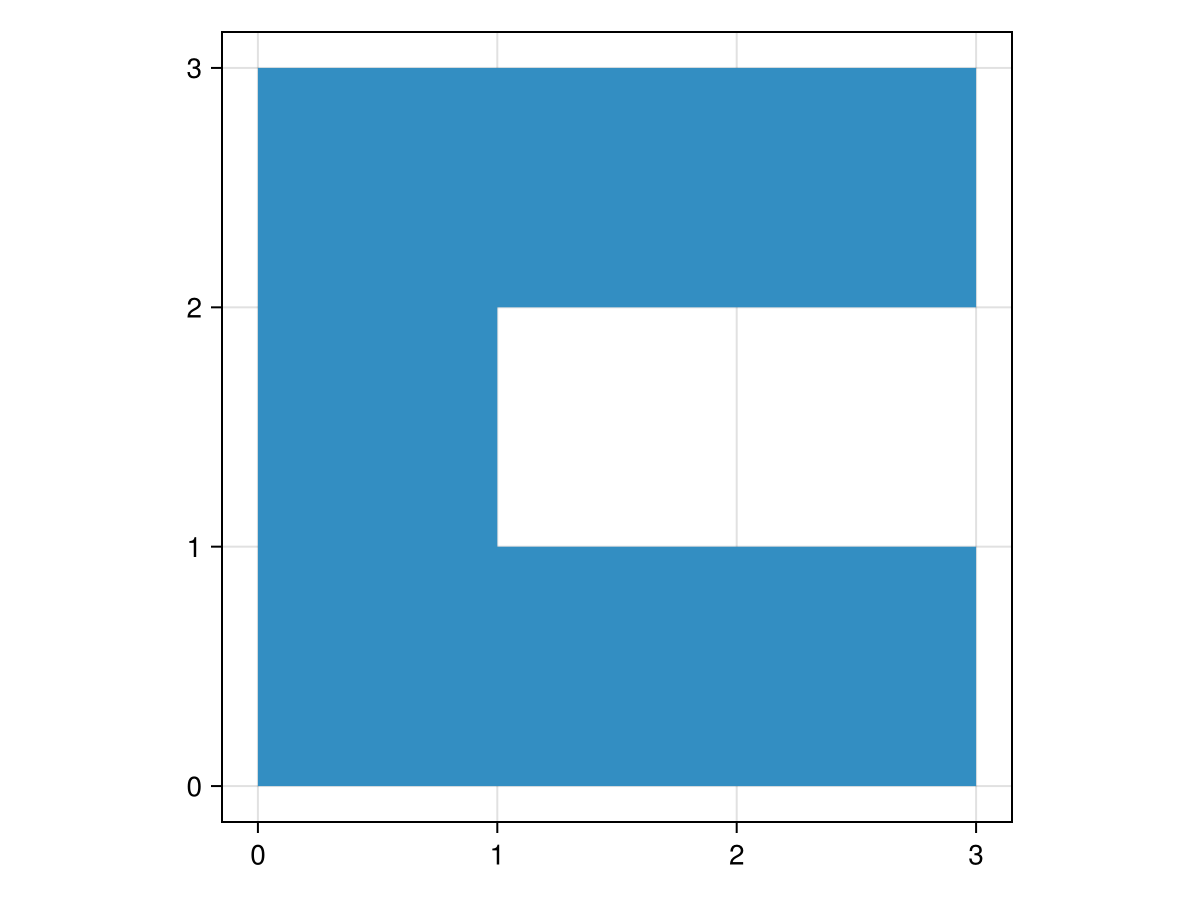

Let's see what the centroid looks like (plotted in red):

cent = GO.centroid(cshape)
scatter!(GI.x(cent), GI.y(cent), color = :red)
f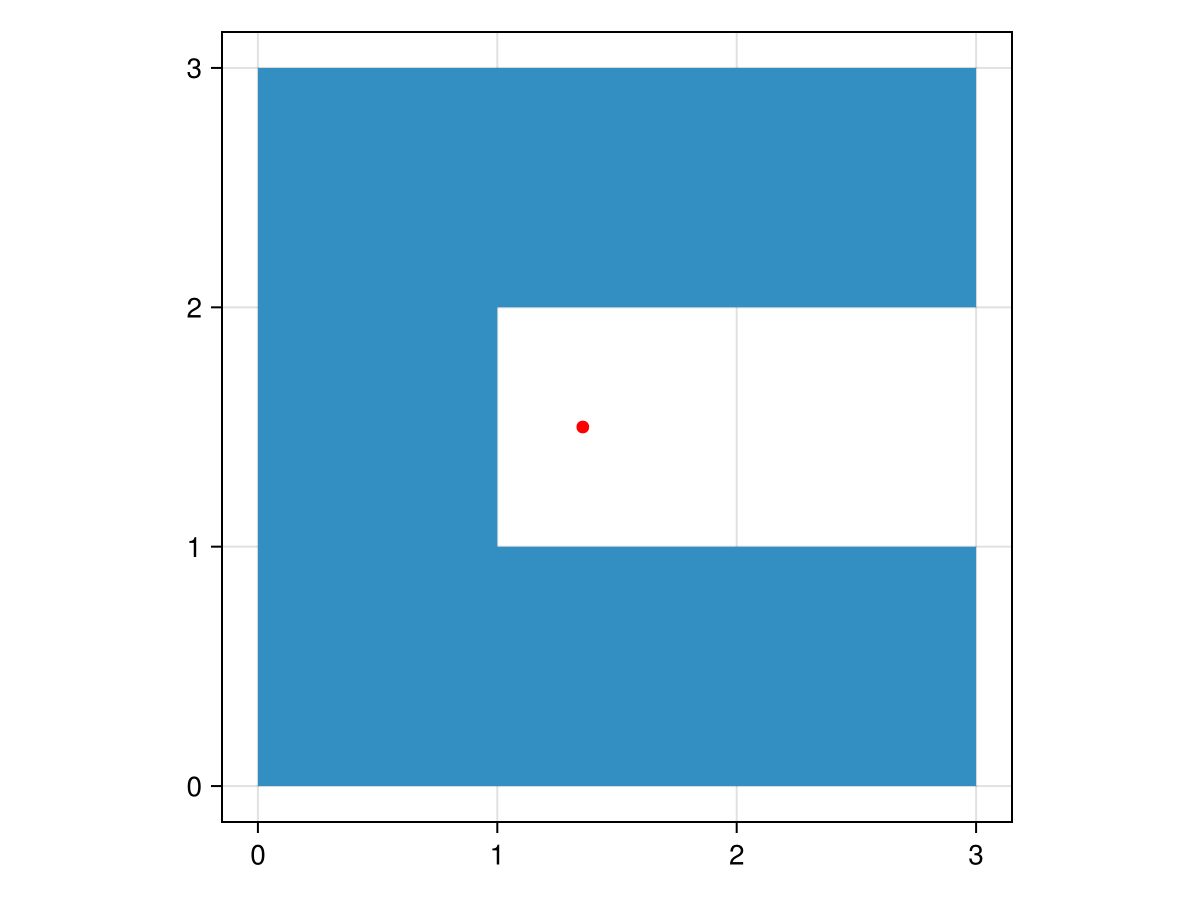

Implementation

This is the GeoInterface-compatible implementation.

First, we implement a wrapper method that dispatches to the correct implementation based on the geometry trait. This is also used in the implementation, since it's a lot less work!

Note that if you call centroid on a LineString or LinearRing, the centroid_and_length function will be called due to the weighting scheme described above, while centroid_and_area is called for polygons and multipolygons. However, centroid_and_area can still be called on a LineString or LinearRing when they are closed, for example as the interior hole of a polygon.

The helper functions centroid_and_length and centroid_and_area are made available just in case the user also needs the area or length to decrease repeat computation.

"""
    centroid(geom, [T=Float64])::Tuple{T, T}

Returns the centroid of a given line segment, linear ring, polygon, or
mutlipolygon.
"""
centroid(geom, ::Type{T} = Float64; threaded=false) where T =
    centroid(GI.trait(geom), geom, T; threaded)
function centroid(
    trait::Union{GI.LineStringTrait, GI.LinearRingTrait}, geom, ::Type{T}=Float64; threaded=false
) where T
    centroid_and_length(trait, geom, T)[1]
end
centroid(trait, geom, ::Type{T}; threaded=false) where T =
    centroid_and_area(trait, geom, T; threaded)[1]

"""
    centroid_and_length(geom, [T=Float64])::(::Tuple{T, T}, ::Real)

Returns the centroid and length of a given line/ring. Note this is only valid
for line strings and linear rings.
"""
centroid_and_length(geom, ::Type{T}=Float64) where T =
    centroid_and_length(GI.trait(geom), geom, T)
function centroid_and_length(
    ::Union{GI.LineStringTrait, GI.LinearRingTrait}, geom, ::Type{T},
) where T

Initialize starting values

    xcentroid = zero(T)
    ycentroid = zero(T)
    length = zero(T)
    point₁ = GI.getpoint(geom, 1)

Loop over line segments of line string

    for point₂ in GI.getpoint(geom)

Calculate length of line segment

        length_component = sqrt(
            (GI.x(point₂) - GI.x(point₁))^2 +
            (GI.y(point₂) - GI.y(point₁))^2
        )

Accumulate the line segment length into length

        length += length_component

Weighted average of line segment centroids

        xcentroid += (GI.x(point₁) + GI.x(point₂)) * (length_component / 2)
        ycentroid += (GI.y(point₁) + GI.y(point₂)) * (length_component / 2)
        #centroid = centroid .+ ((point₁ .+ point₂) .* (length_component / 2))

Advance the point buffer by 1 point to move to next line segment

        point₁ = point₂
    end
    xcentroid /= length
    ycentroid /= length
    return (xcentroid, ycentroid), length
end

"""
    centroid_and_area(geom, [T=Float64])::(::Tuple{T, T}, ::Real)

Returns the centroid and area of a given geometry.
"""
function centroid_and_area(geom, ::Type{T}=Float64; threaded=false) where T
    trait = GI.trait(geom)
    centroid_and_area(trait, geom, T; threaded)
end

function centroid_and_area(trait, geom, ::Type{T}; threaded=false) where T
    target = TraitTarget{Union{GI.PolygonTrait,GI.LineStringTrait,GI.LinearRingTrait}}()
    init = (zero(T), zero(T)), zero(T)
    applyreduce(WithTrait((trait, g) -> centroid_and_area(trait, g, T)), _combine_centroid_and_area, target, geom; threaded, init)
end

function centroid_and_area(
    ::Union{GI.LineStringTrait, GI.LinearRingTrait}, geom, ::Type{T}
) where T

Check that the geometry is closed

    @assert(
        GI.getpoint(geom, 1) == GI.getpoint(geom, GI.ngeom(geom)),
        "centroid_and_area should only be used with closed geometries"
    )

Initialize starting values

    xcentroid = zero(T)
    ycentroid = zero(T)
    area = zero(T)
    point₁ = GI.getpoint(geom, 1)

Loop over line segments of linear ring

    for point₂ in GI.getpoint(geom)
        area_component = GI.x(point₁) * GI.y(point₂) -
            GI.x(point₂) * GI.y(point₁)

Accumulate the area component into area

        area += area_component

Weighted average of centroid components

        xcentroid += (GI.x(point₁) + GI.x(point₂)) * area_component
        ycentroid += (GI.y(point₁) + GI.y(point₂)) * area_component

Advance the point buffer by 1 point

        point₁ = point₂
    end
    area /= 2
    xcentroid /= 6area
    ycentroid /= 6area
    return (xcentroid, ycentroid), abs(area)
end
function centroid_and_area(::GI.PolygonTrait, geom, ::Type{T}) where T

Exterior ring's centroid and area

    exterior = GI.getexterior(geom)
    (xcentroid, ycentroid), area = centroid_and_area(GI.geomtrait(exterior), exterior, T)

Weight exterior centroid by area

    xcentroid *= area
    ycentroid *= area

Loop over any holes within the polygon

    for hole in GI.gethole(geom)

Hole polygon's centroid and area

        (xinterior, yinterior), interior_area = centroid_and_area(GI.geomtrait(hole), hole, T)

Accumulate the area component into area

        area -= interior_area

Weighted average of centroid components

        xcentroid -= xinterior * interior_area
        ycentroid -= yinterior * interior_area
    end
    xcentroid /= area
    ycentroid /= area
    return (xcentroid, ycentroid), area
end

The op argument for _applyreduce and point / area It combines two (point, area) tuples into one, taking the average of the centroid points weighted by the area of the geom they are from.

function _combine_centroid_and_area(((x1, y1), area1), ((x2, y2), area2))
    area = area1 + area2
    x = (x1 * area1 + x2 * area2) / area
    y = (y1 * area1 + y2 * area2) / area
    return (x, y), area
end

---

This page was generated using Literate.jl.