Creating Geometry

In this tutorial, we're going to:

1. Create and plot geometries

2. Plot geometries on a map using GeoMakie and coordinate reference system (CRS)

3. Create geospatial geometries with embedded coordinate reference system information

4. Assign attributes to geospatial geometries

5. Save geospatial geometries to common geospatial file formats

First, we load some required packages.

# Geospatial packages from Julia
import GeoInterface as GI
import GeometryOps as GO
import GeoFormatTypes as GFT
using GeoJSON # to load some data
# Packages for coordinate transformation and projection
import CoordinateTransformations
import Proj
# Plotting
using CairoMakie
using GeoMakie

Precompiling packages...
   1547.4 ms  ✓ Geodesy
   8614.8 ms  ✓ GeoMakie
  2 dependencies successfully precompiled in 10 seconds. 286 already precompiled.
Precompiling packages...
    915.4 ms  ✓ DisplayAs
  1 dependency successfully precompiled in 1 seconds

Creating and plotting geometries

Let's start by making a single Point.

point = GI.Point(0, 0)

Point{false, false}((0, 0))

Now, let's plot our point.

fig, ax, plt = plot(point)

Let's create a set of points, and have a bit more fun with plotting.

x = [-5, 0, 5, 0];
y = [0, -5, 0, 5];
points = GI.Point.(zip(x,y));
plot!(ax, points; marker = '✈', markersize = 30)
fig

Points can be combined into a single MultiPoint geometry.

x = [-5, -5, 5, 5];
y = [-5, 5, 5, -5];
multipoint = GI.MultiPoint(GI.Point.(zip(x, y)));
# TODO: GeoInterfaceMakie.jl can't plot multipoints due to breaking changes
# in Makie.jl.  We should fix that.
plot!(ax, multipoint.geom; marker = '☁', markersize = 30)
fig

Let's create a LineString connecting two points.

p1 = GI.Point.(-5, 0);
p2 = GI.Point.(5, 0);
line = GI.LineString([p1,p2])
plot!(ax, line; color = :red)
fig

Now, let's create a line connecting multiple points (i.e. a LineString). This time we get a bit more fancy with point creation.

r = 2;
k = 10;
ϴ = 0:0.01:2pi;
x = r .* (k + 1) .* cos.(ϴ) .- r .* cos.((k + 1) .* ϴ);
y = r .* (k + 1) .* sin.(ϴ) .- r .* sin.((k + 1) .* ϴ);
lines = GI.LineString(GI.Point.(zip(x,y)));
plot!(ax, lines; linewidth = 5)
fig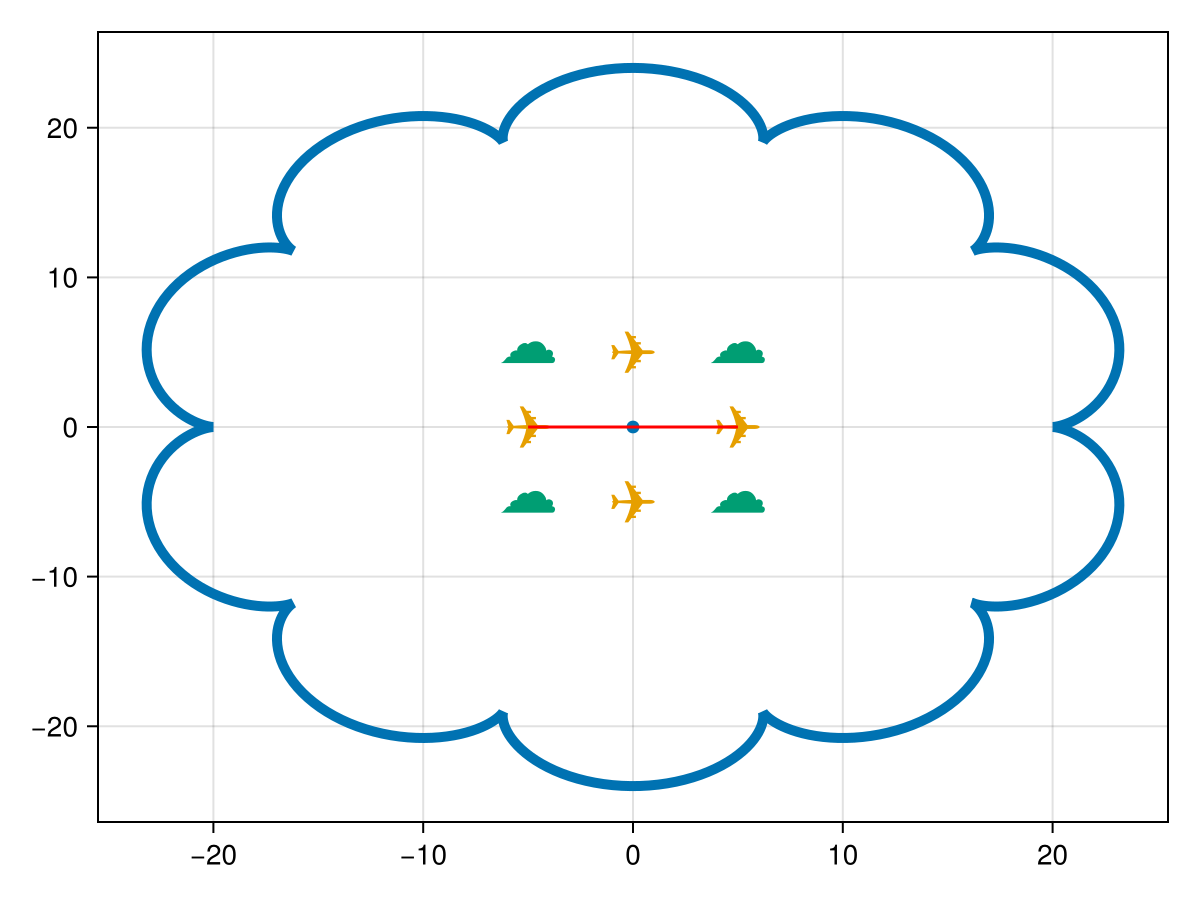

We can also create a single LinearRing trait, the building block of a polygon. A LinearRing is simply a LineString with the same beginning and endpoint, i.e., an arbitrary closed shape composed of point pairs.

A LinearRing is composed of a series of points.

ring1 = GI.LinearRing(GI.getpoint(lines));

GeoInterface.Wrappers.LinearRing{false, false}([Point((20.0, 0.0)), … (627) … , Point((20.001115954499138, -1.4219350464667047e-5))])

Now, let's make the LinearRing into a Polygon.

polygon1 = GI.Polygon([ring1]);

GeoInterface.Wrappers.Polygon{false, false}([GeoInterface.Wrappers.LinearRing([Point((20.0, 0.0)), … (627) … , Point((20.001115954499138, -1.4219350464667047e-5))])])

Now, we can use GeometryOps and CoordinateTransformations to shift polygon1 up, to avoid plotting over our earlier results. This is done through the GeometryOps.transform function.

xoffset = 0.;
yoffset = 50.;
f = CoordinateTransformations.Translation(xoffset, yoffset);
polygon1 = GO.transform(f, polygon1);
plot!(polygon1)
fig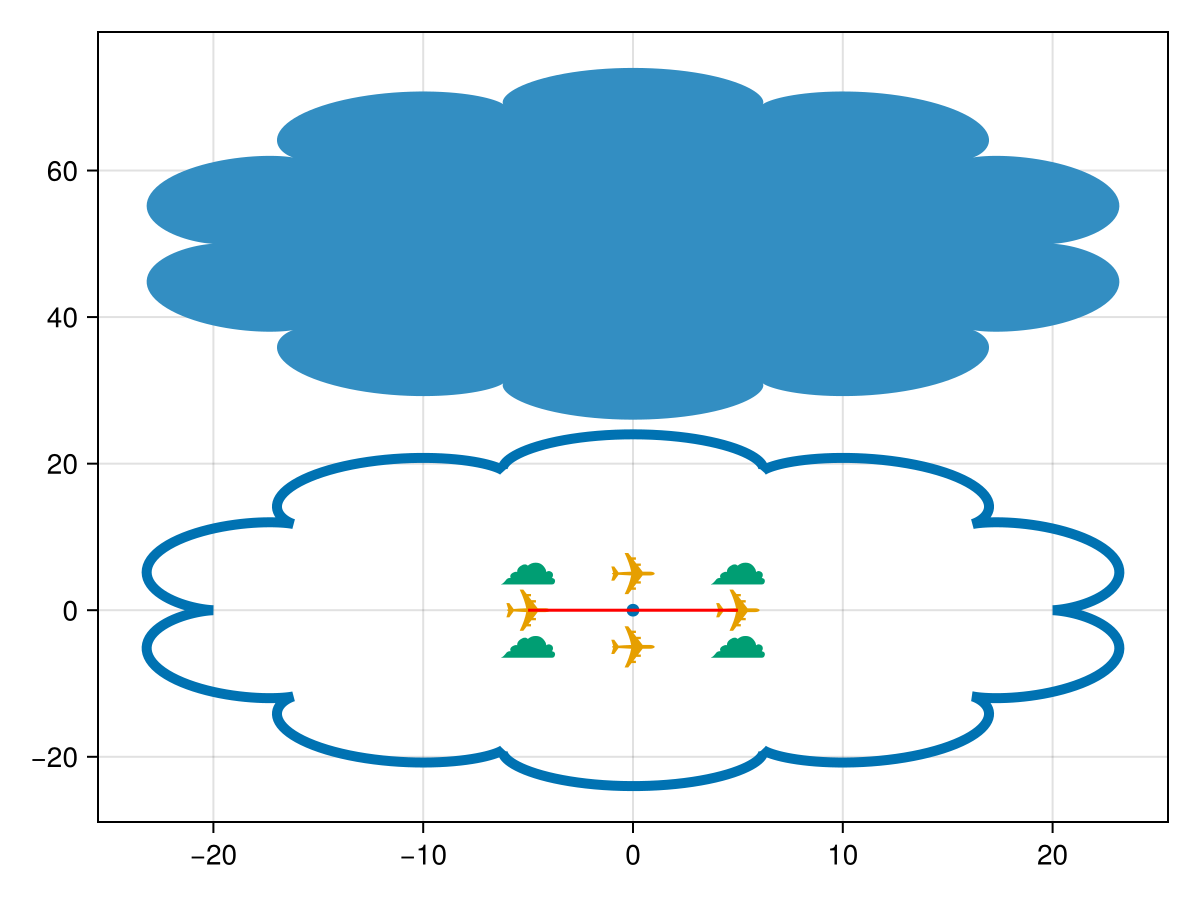

Polygons can contain "holes". The first LinearRing in a polygon is the exterior, and all subsequent LinearRings are treated as holes in the leading LinearRing.

GeoInterface offers the GI.getexterior(poly) and GI.gethole(poly) methods to get the exterior ring and an iterable of holes, respectively.

hole = GI.LinearRing(GI.getpoint(multipoint))
polygon2 = GI.Polygon([ring1, hole])

GeoInterface.Wrappers.Polygon{false, false}([GeoInterface.Wrappers.LinearRing([Point((20.0, 0.0)), … (627) … , Point((20.001115954499138, -1.4219350464667047e-5))]), GeoInterface.Wrappers.LinearRing([Point((-5, -5)), … (2) … , Point((5, -5))])])

Shift polygon2 to the right, to avoid plotting over our earlier results.

xoffset = 50.;
yoffset = 0.;
f = CoordinateTransformations.Translation(xoffset, yoffset);
polygon2 = GO.transform(f, polygon2);
plot!(polygon2)
fig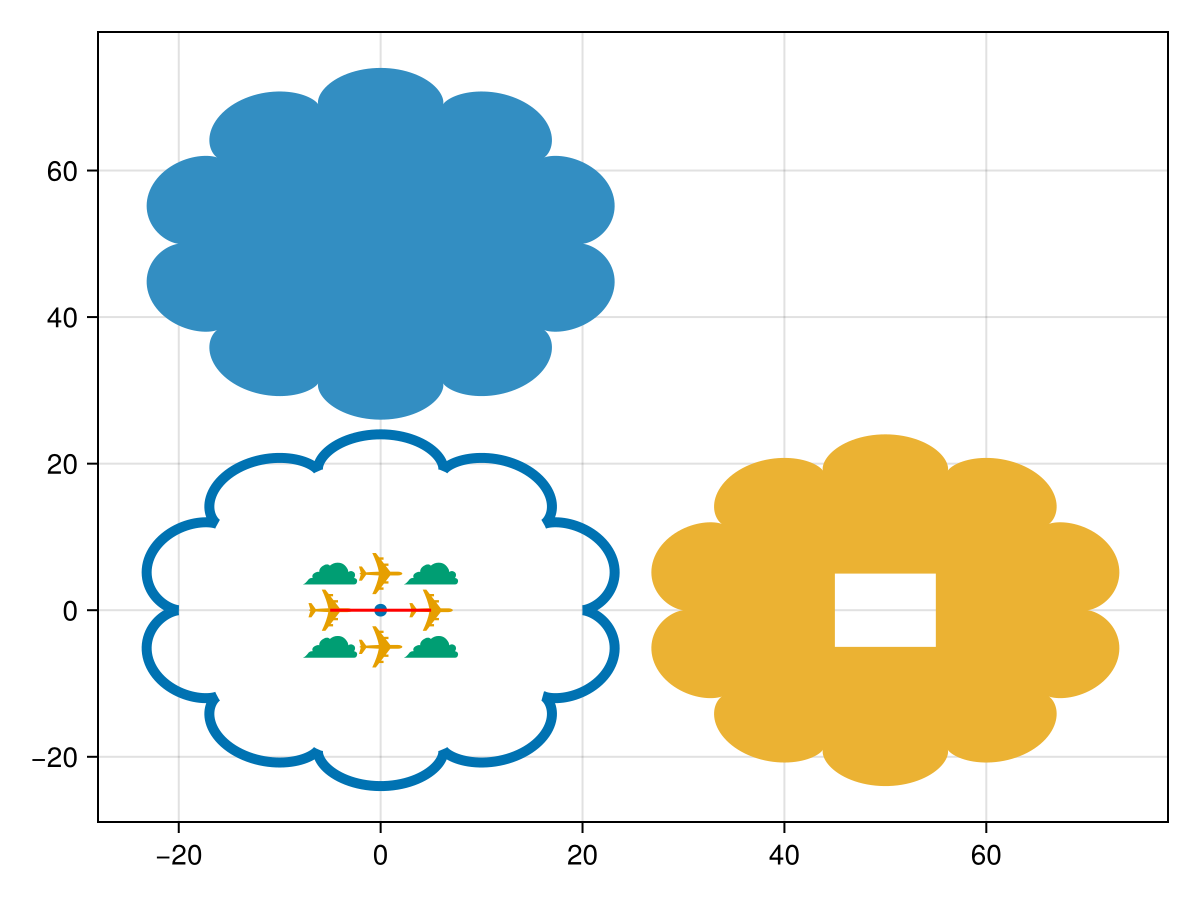

Polygons can also be grouped together as a MultiPolygon.

r = 5;
x = cos.(reverse(ϴ)) .* r .+ xoffset;
y = sin.(reverse(ϴ)) .* r .+ yoffset;
ring2 =  GI.LinearRing(GI.Point.(zip(x,y)));
polygon3 = GI.Polygon([ring2]);
multipolygon = GI.MultiPolygon([polygon2, polygon3])

GeoInterface.Wrappers.MultiPolygon{false, false}([GeoInterface.Wrappers.Polygon([GeoInterface.Wrappers.LinearRing([[70.0, 0.0], … (627) … , [70.00111595449914, -1.4219350464667047e-5]]), GeoInterface.Wrappers.LinearRing([[45.0, -5.0], … (2) … , [55.0, -5.0]])]), GeoInterface.Wrappers.Polygon([GeoInterface.Wrappers.LinearRing([Point((54.999974634566875, -0.01592650896568995)), … (627) … , Point((55.0, 0.0))])])])

Shift multipolygon up, to avoid plotting over our earlier results.

xoffset = 0.;
yoffset = 50.;
f = CoordinateTransformations.Translation(xoffset, yoffset);
multipolygon = GO.transform(f, multipolygon);
plot!(multipolygon)
fig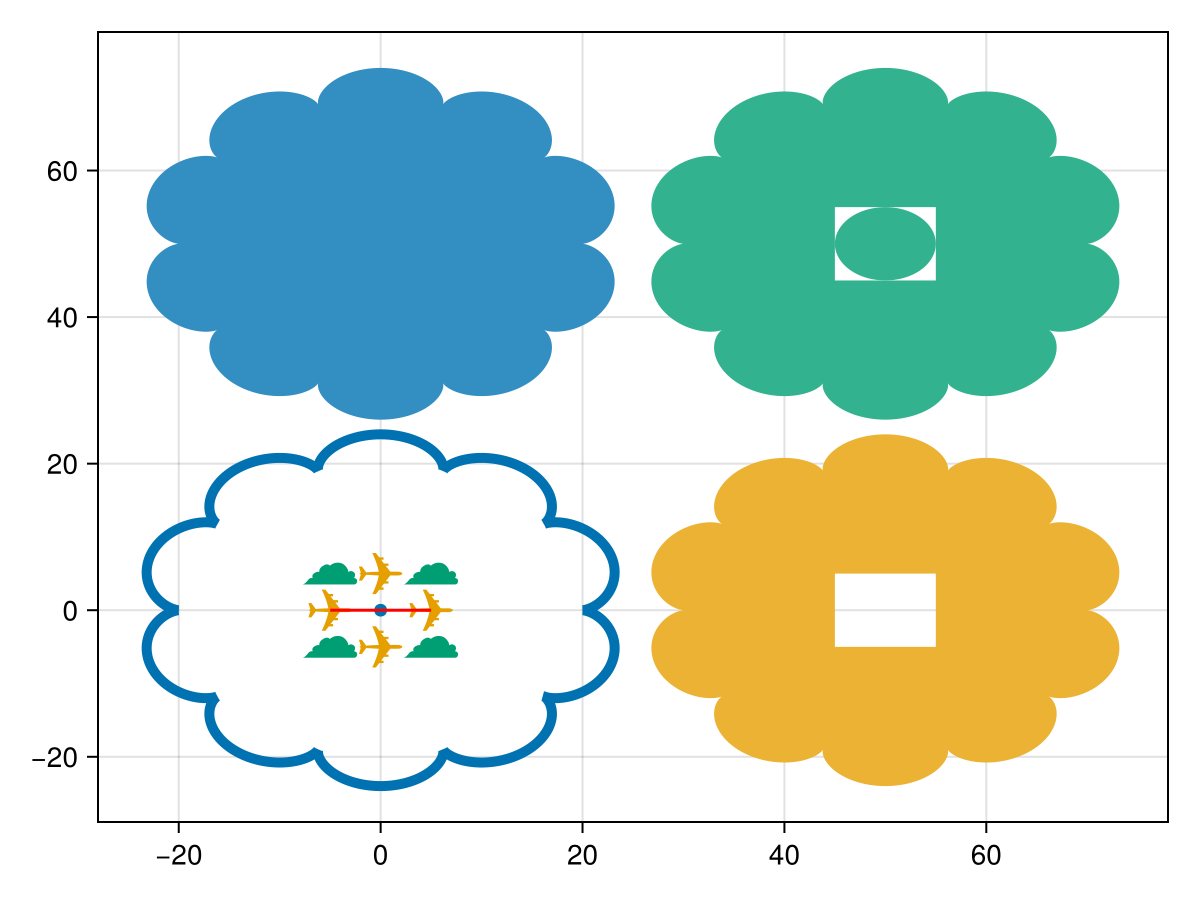

Great, now we can make Points, MultiPoints, Lines, LineStrings, Polygons (with holes), and MultiPolygons and modify them using [CoordinateTransformations] and [GeometryOps].

Plot geometries on a map using GeoMakie and coordinate reference system (CRS)

In geospatial sciences we often have data in one Coordinate Reference System (CRS) (source) and would like to display it in different (destination) CRS. GeoMakie allows us to do this by automatically projecting from source to destination CRS.

Here, our source CRS is common geographic (i.e. coordinates of latitude and longitude), WGS84.

source_crs1 = GFT.EPSG(4326)

EPSG:4326

Now let's pick a destination CRS for displaying our map. Here we'll pick natearth2.

destination_crs = "+proj=natearth2"

"+proj=natearth2"

Let's add land area for context. First, download and open the Natural Earth global land polygons at 110 m resolution.GeoMakie ships with this particular dataset, so we will access it from there.

land_path = GeoMakie.assetpath("ne_110m_land.geojson")

"/home/runner/.julia/dev/GeoMakie/assets/ne_110m_land.geojson"

Note

Natural Earth has lots of other datasets, and there is a Julia package that provides an interface to it called NaturalEarth.jl.

Read the land MultiPolygons as a GeoJSON.FeatureCollection.

land_geo = GeoJSON.read(land_path)

FeatureCollection with 127 Features

We then need to create a figure with a GeoAxis that can handle the projection between source and destination CRS. For GeoMakie, source is the CRS of the input and dest is the CRS you want to visualize in.

fig = Figure(size=(1000, 500));
ga = GeoAxis(
    fig[1, 1];
    source = source_crs1,
    dest = destination_crs,
    xticklabelsvisible = false,
    yticklabelsvisible = false,
);

Plot land for context.

poly!(ga, land_geo, color=:black)
fig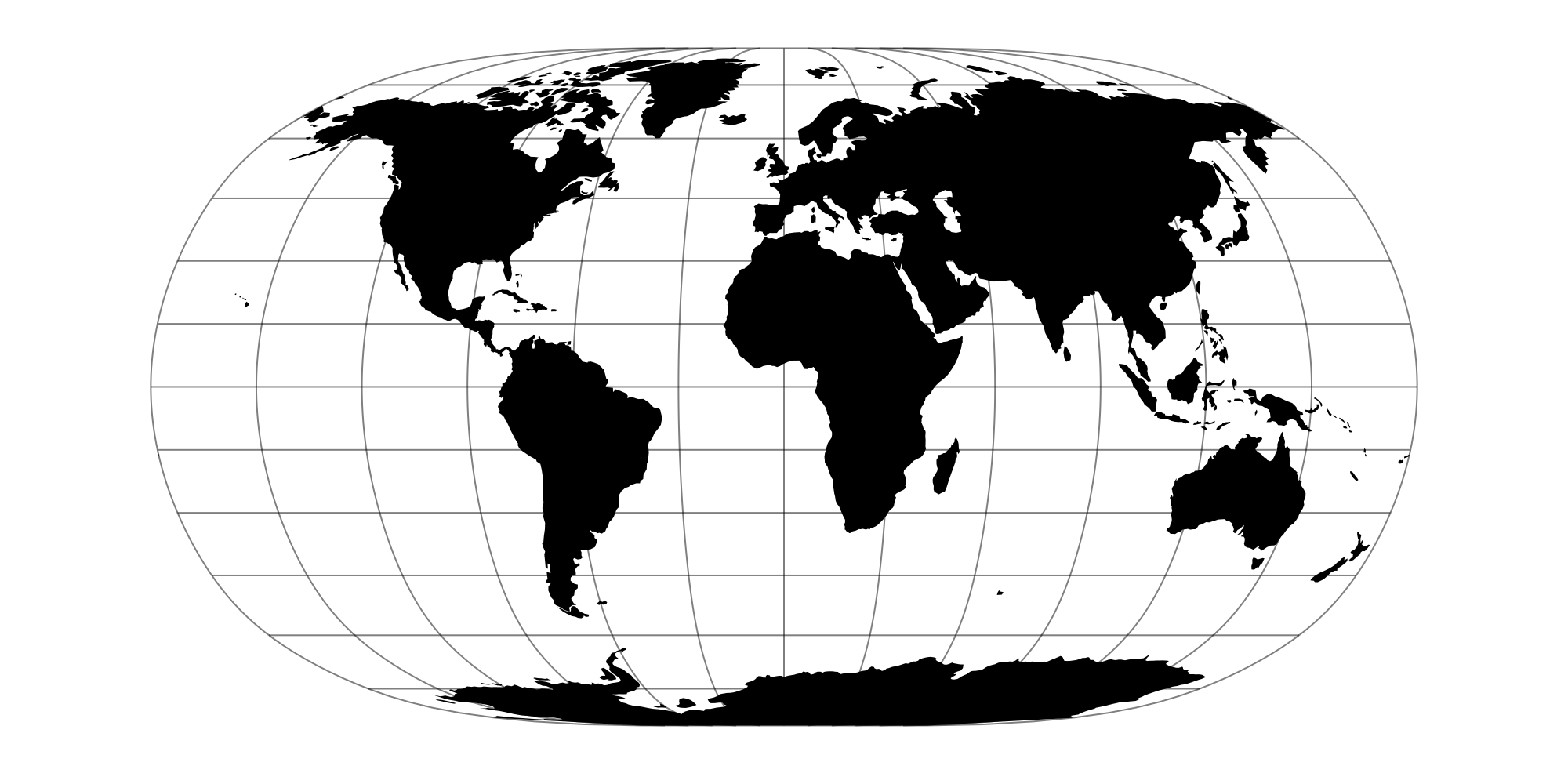

Now let's plot a Polygon like before, but this time with a CRS that differs from our source data

plot!(multipolygon; color = :green)
fig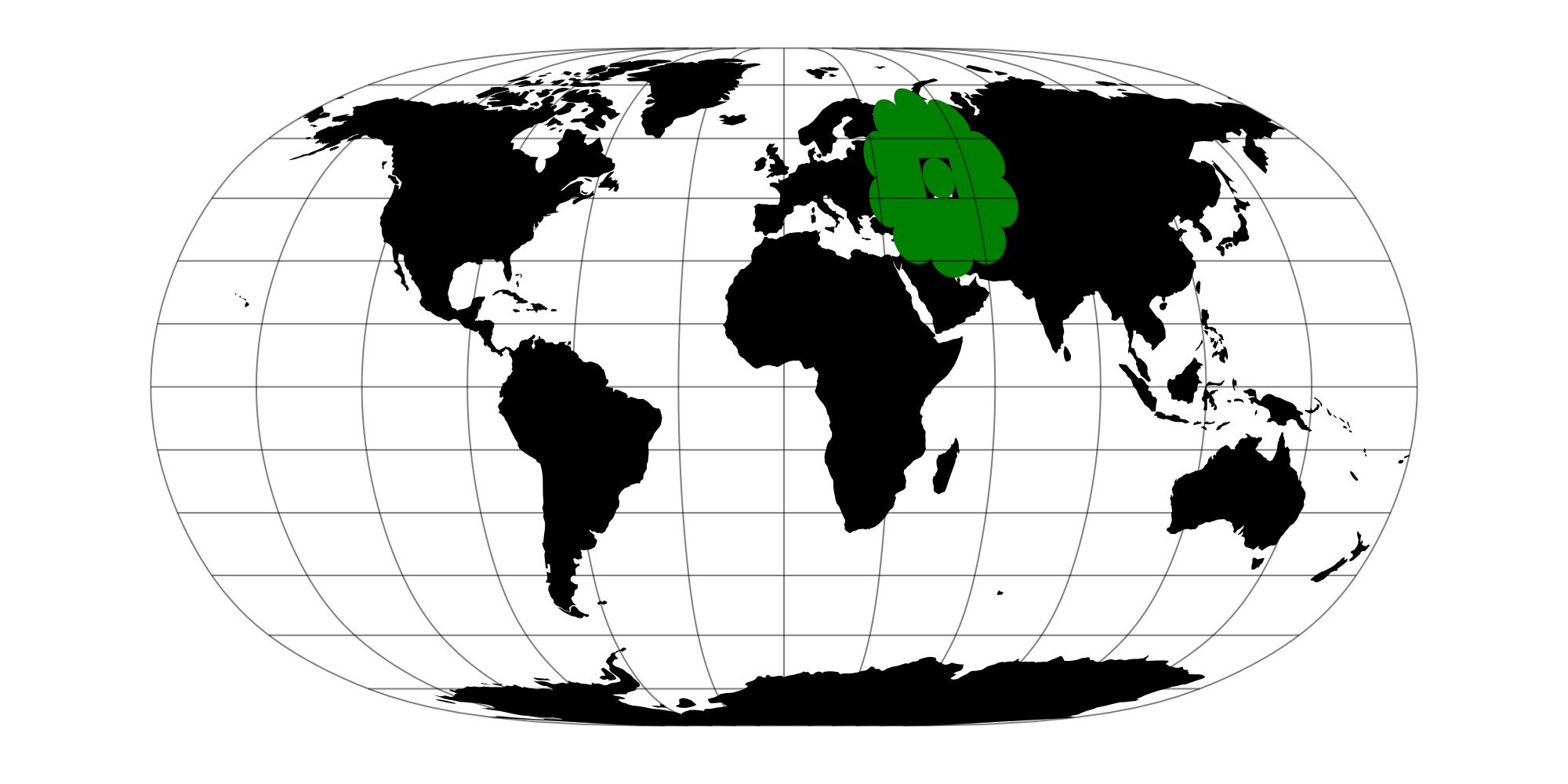

But what if we want to plot geometries with a different source CRS on the same figure?

To show how to do this let's create a geometry with coordinates in UTM (Universal Transverse Mercator) zone 10N EPSG:32610.

source_crs2 = GFT.EPSG(32610)

EPSG:32610

Create a polygon (we're working in meters now, not latitude and longitude)

r = 1000000;
ϴ = 0:0.01:2pi;
x = r .* cos.(ϴ).^3 .+ 500000;
y = r .* sin.(ϴ) .^ 3 .+5000000;

629-element Vector{Float64}:
 5.0e6
 5.0e6
 5.00001e6
 ⋮
 5.0e6
 5.0e6

Now create a LinearRing from Points

ring3 = GI.LinearRing(Point.(zip(x, y)))

GeoInterface.Wrappers.LinearRing{false, false}([[1.5e6, 5.0e6], … (627) … , [1.499984780817334e6, 4.999999967681458e6]])

Now create a Polygon from the LineRing

polygon3 = GI.Polygon([ring3])

GeoInterface.Wrappers.Polygon{false, false}([GeoInterface.Wrappers.LinearRing([[1.5e6, 5.0e6], … (627) … , [1.499984780817334e6, 4.999999967681458e6]])])

Now plot on the existing GeoAxis.

Note

The keyword argument source is used to specify the source CRS of that particular plot, when plotting on an existing GeoAxis.

plot!(ga,polygon3; color=:red, source = source_crs2)
fig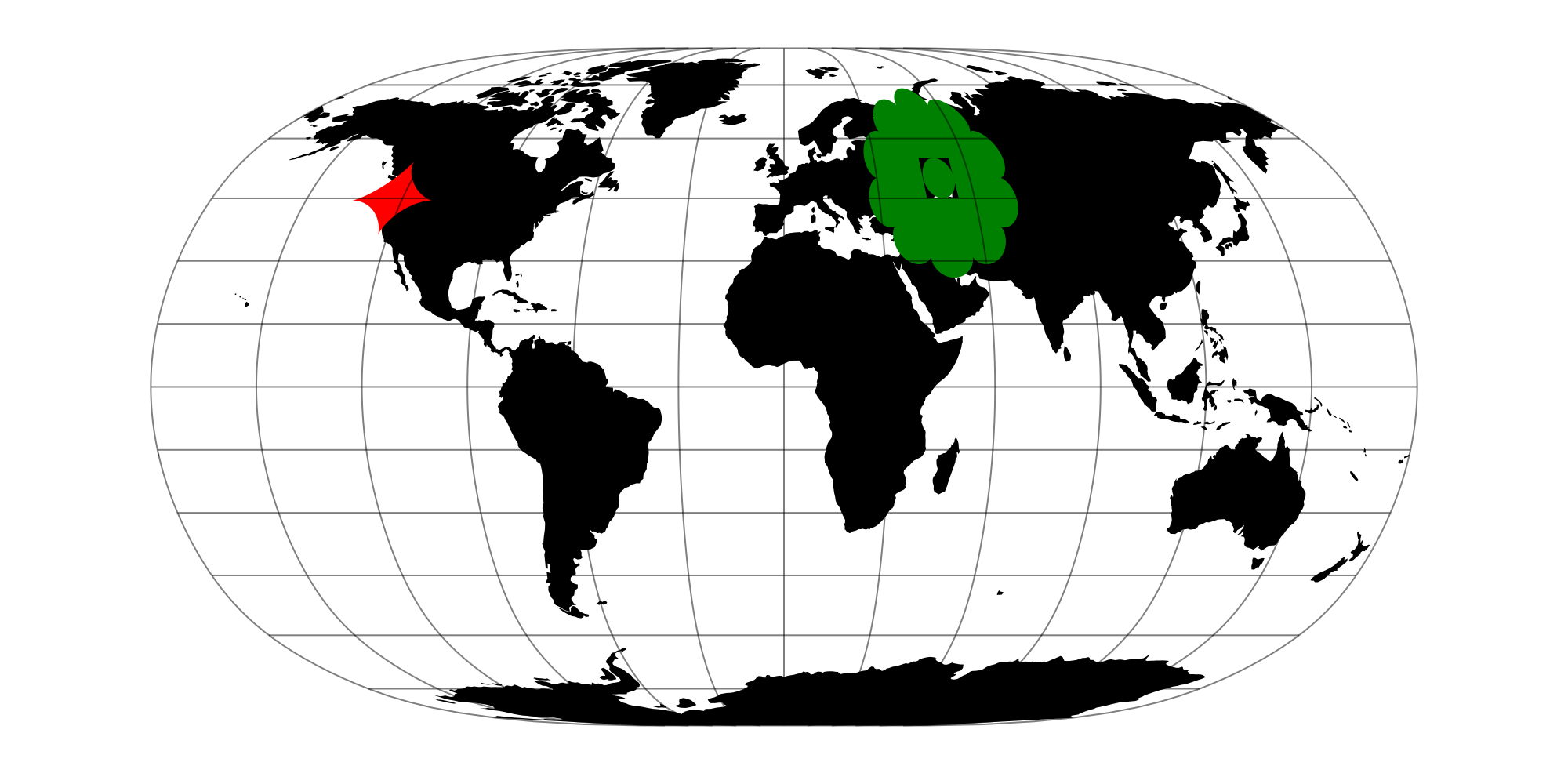

Create geospatial geometries with embedded coordinate reference system information

Great, we can make geometries and plot them on a map... now let's export the data to common geospatial data formats. To do this we now need to create geometries with embedded CRS information, making it a geospatial geometry. All that's needed is to include ; crs = crs as a keyword argument when constructing the geometry.

Let's do this for a new Polygon

r = 3;
k = 7;
ϴ = 0:0.01:2pi;
x = r .* (k + 1) .* cos.(ϴ) .- r .* cos.((k + 1) .* ϴ);
y = r .* (k + 1) .* sin.(ϴ) .- r .* sin.((k + 1) .* ϴ);
ring4 = GI.LinearRing(Point.(zip(x, y)))

GeoInterface.Wrappers.LinearRing{false, false}([[21.0, 0.0], … (627) … , [21.00085222666982, -8.14404531208901e-6]])

But this time when we create the Polygon we need to specify the CRS at the time of creation, making it a geospatial polygon

geopoly1 = GI.Polygon([ring4], crs = source_crs1)

GeoInterface.Wrappers.Polygon{false, false}([GeoInterface.Wrappers.LinearRing([[21.0, 0.0], … (627) … , [21.00085222666982, -8.14404531208901e-6]])], crs = "EPSG:4326")

Note

It is good practice to only include CRS information with the highest-level geometry. Not doing so can bloat the memory footprint of the geometry. CRS information can be included at the individual Point level but is discouraged.

And let's create second Polygon by shifting the first using CoordinateTransformations

xoffset = 20.;
yoffset = -25.;
f = CoordinateTransformations.Translation(xoffset, yoffset);
geopoly2 = GO.transform(f, geopoly1);

GeoInterface.Wrappers.Polygon{false, false}([GeoInterface.Wrappers.LinearRing([[41.0, -25.0], … (627) … , [41.00085222666982, -25.000008144045314]], crs = "EPSG:4326")], crs = "EPSG:4326")

Creating a table with attributes and geometry

Typically, you'll also want to include attributes with your geometries. Attributes are simply data that are attributed to each geometry. The easiest way to do this is to create a table with a :geometry column. Let's do this using DataFrames.

using DataFrames
df = DataFrame(geometry=[geopoly1, geopoly2])

2×1 DataFrame

Row	geometry
	Polygon…
1	GeoInterface.Wrappers.Polygon([GeoInterface.Wrappers.LinearRing([[21.0,0.0],…(627)…,[21.00085222666982,-8.14404531208901e-6]])])
2	GeoInterface.Wrappers.Polygon([GeoInterface.Wrappers.LinearRing([[41.0,-25.0],…(627)…,[41.00085222666982,-25.000008144045314]])])

Now let's add a couple of attributes to the geometries. We do this using DataFrames' ! mutation syntax that allows you to add a new column to an existing data frame.

df[!,:id] = ["a", "b"]
df[!, :name] = ["polygon 1", "polygon 2"]
df

2×3 DataFrame

Row	geometry	id	name
	Polygon…	String	String
1	GeoInterface.Wrappers.Polygon([GeoInterface.Wrappers.LinearRing([[21.0,0.0],…(627)…,[21.00085222666982,-8.14404531208901e-6]])])	a	polygon 1
2	GeoInterface.Wrappers.Polygon([GeoInterface.Wrappers.LinearRing([[41.0,-25.0],…(627)…,[41.00085222666982,-25.000008144045314]])])	b	polygon 2

Saving your geospatial data

There are Julia packages for most commonly used geographic data formats. Below, we show how to export that data to each of these.

We begin with GeoJSON, which is a JSON format for geospatial feature collections. It's human-readable and widely supported by most web-based and desktop geospatial libraries.

import GeoJSON
fn = "shapes.json"
GeoJSON.write(fn, df)

"shapes.json"

Now, let's save as a Shapefile. Shapefiles are actually a set of files (usually 4) that hold geometry information, a CRS, and additional attribute information as a separate table. When you give Shapefile.write a file name, it will write 4 files of the same name but with different extensions.

import Shapefile
fn = "shapes.shp"
Shapefile.write(fn, df)

20340

Now, let's save as a GeoParquet. GeoParquet is a geospatial extension to the Parquet format, which is a high-performance data store. It's great for storing large amounts of data in a single file.

import GeoParquet
fn = "shapes.parquet"
GeoParquet.write(fn, df, (:geometry,))

"shapes.parquet"

Finally, if there's no Julia-native package that can write data to your desired format (e.g. .gpkg, .gml, etc), you can use GeoDataFrames. This package uses the GDAL library under the hood which supports writing to nearly all geospatial formats.

import GeoDataFrames
fn = "shapes.gpkg"
GeoDataFrames.write(fn, df)

"shapes.gpkg"

And there we go, you can now create mapped geometries from scratch, manipulate them, plot them on a map, and save them in multiple geospatial data formats.