Convex hull

The convex hull of a set of points is the smallest convex polygon that contains all the points.

GeometryOps.jl provides a number of methods for computing the convex hull of a set of points, usually linked to other Julia packages.

For now, we expose one algorithm, MonotoneChainMethod, which uses the DelaunayTriangulation.jl package. The GEOS() interface also supports convex hulls.

Future work could include other algorithms, such as Quickhull.jl, or similar, via package extensions.

Example

Simple hull

import GeometryOps as GO, GeoInterface as GI
using CairoMakie # to plot

points = randn(GO.Point2f, 100)
f, a, p = plot(points; label = "Points")
hull_poly = GO.convex_hull(points)
lines!(a, hull_poly; label = "Convex hull", color = Makie.wong_colors()[2])
axislegend(a)
f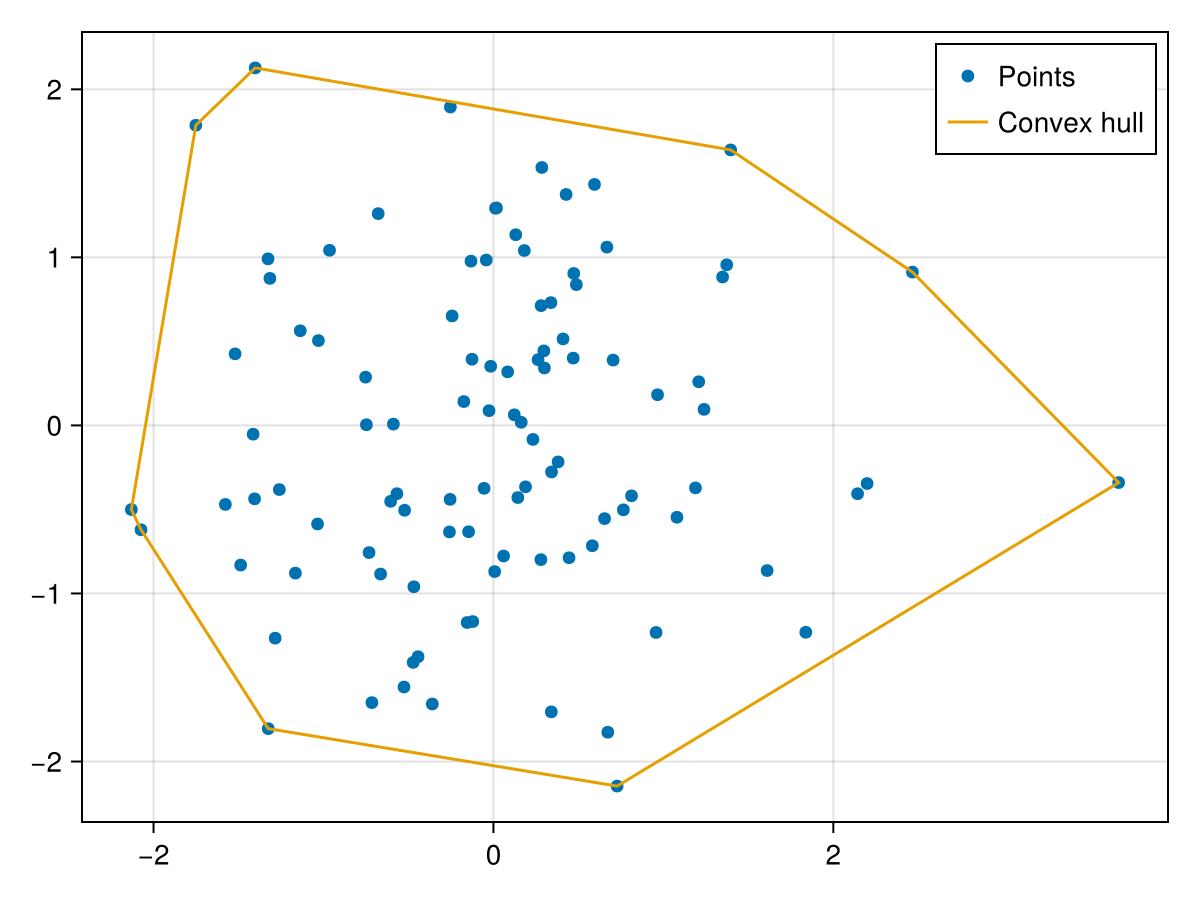

Convex hull of the USA

import GeometryOps as GO, GeoInterface as GI
using CairoMakie # to plot
using NaturalEarth # for data

all_adm0 = naturalearth("admin_0_countries", 110)
usa = all_adm0.geometry[findfirst(==("USA"), all_adm0.ADM0_A3)]
f, a, p = lines(usa)
lines!(a, GO.convex_hull(usa); color = Makie.wong_colors()[2])
f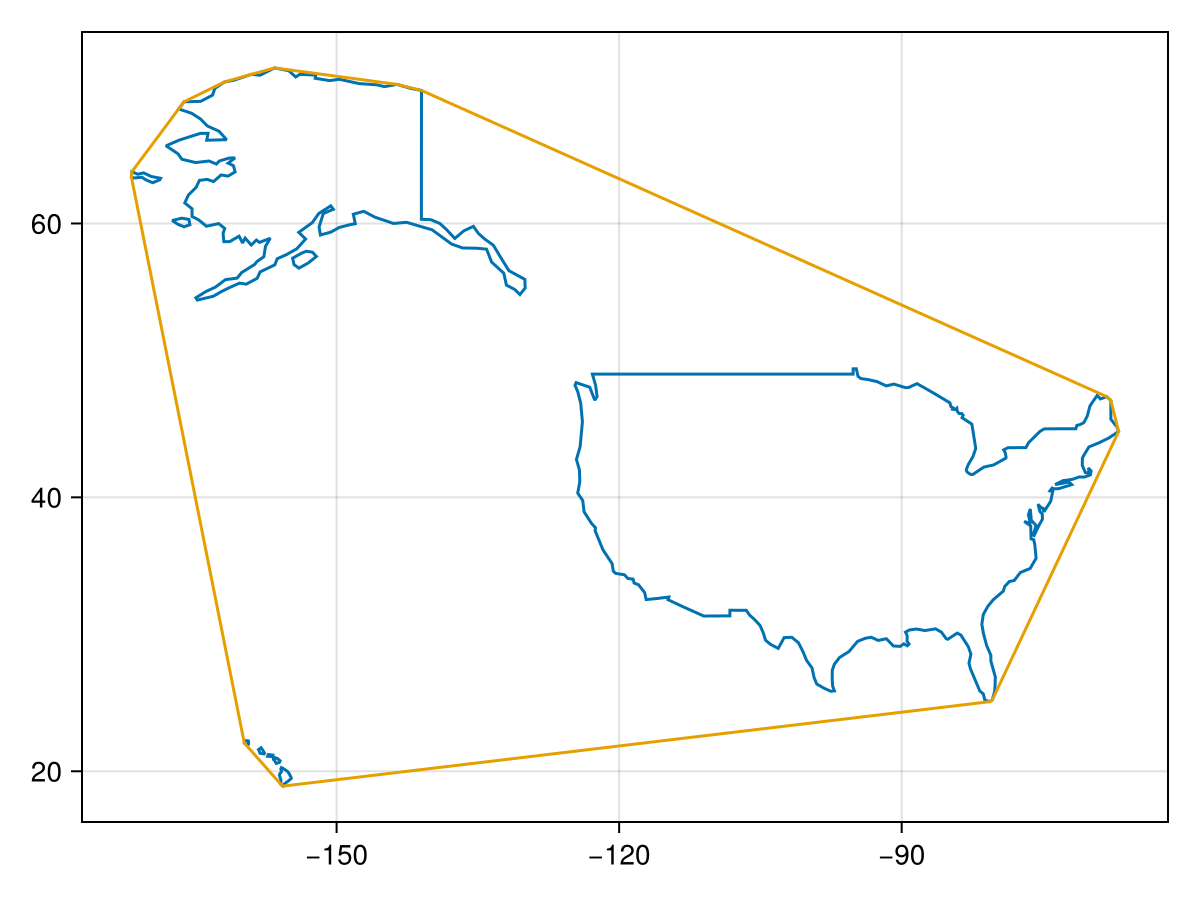

Investigating the winding order

The winding order of the monotone chain method is counterclockwise, while the winding order of the GEOS method is clockwise.

GeometryOps' convexity detection says that the GEOS hull is convex, while the monotone chain method hull is not. However, they are both going over the same points (we checked), it's just that the winding order is different.

In reality, both sets are convex, but we need to fix the GeometryOps convexity detector (isconcave)!

We may also decide at a later date to change the returned winding order of the polygon, but most algorithms are robust to that, and you can always fix it...

import GeoInterface as GI, GeometryOps as GO, LibGEOS as LG
using CairoMakie # to plot

points = rand(Point2{Float64}, 100)
go_hull = GO.convex_hull(GO.MonotoneChainMethod(), points)
lg_hull = GO.convex_hull(GO.GEOS(), points)

fig = Figure()
a1, p1 = lines(fig[1, 1], go_hull; color = 1:GI.npoint(go_hull), axis = (; title = "MonotoneChainMethod()"))
a2, p2 = lines(fig[2, 1], lg_hull; color = 1:GI.npoint(lg_hull), axis = (; title = "GEOS()"))
cb = Colorbar(fig[1:2, 2], p1; label = "Vertex number")
fig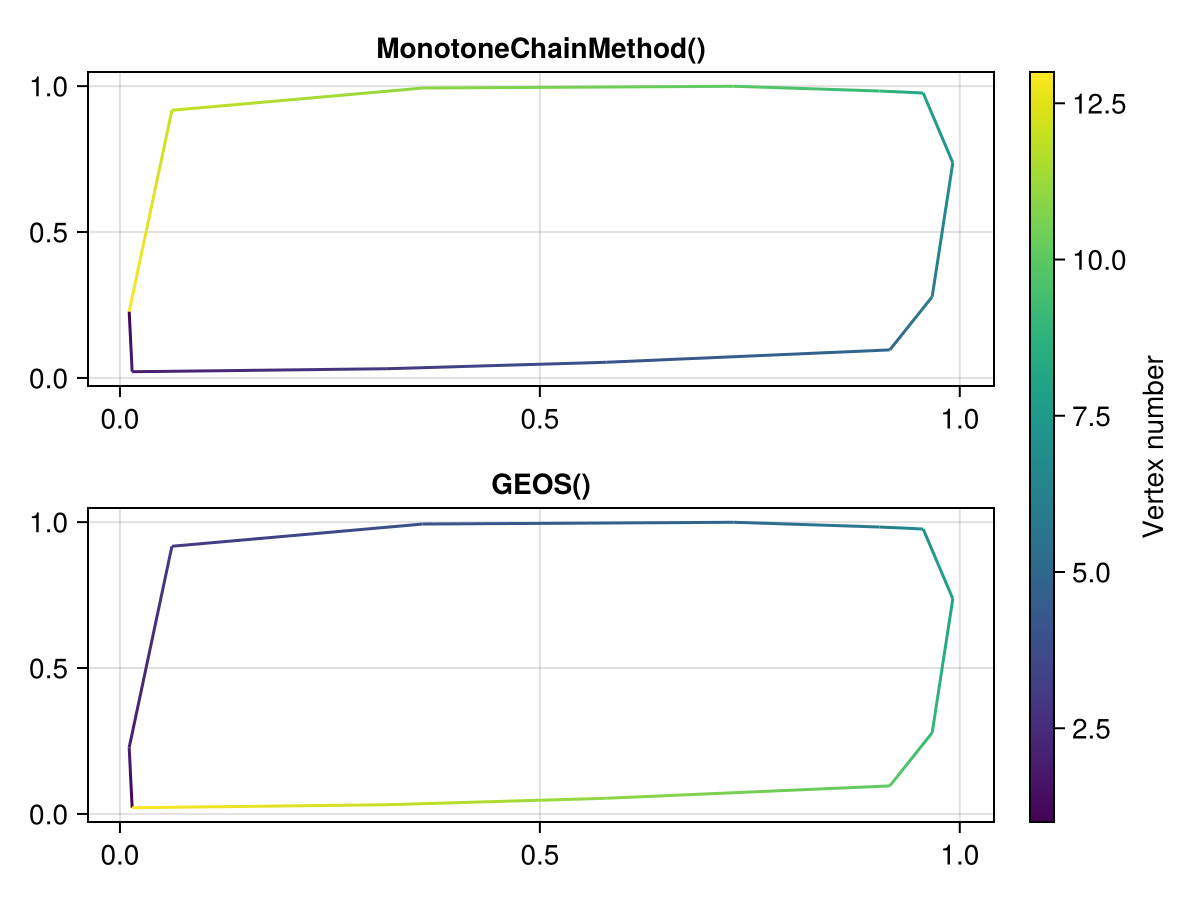

Implementation

"""
    convex_hull([method], geometries)

Compute the convex hull of the points in `geometries`.
Returns a `GI.Polygon` representing the convex hull.

Note that the polygon returned is wound counterclockwise
as in the Simple Features standard by default.  If you
choose GEOS, the winding order will be inverted.

!!! warning
    This interface only computes the 2-dimensional convex hull!

    For higher dimensional hulls, use the relevant package (Qhull.jl, Quickhull.jl, or similar).
"""
function convex_hull end

"""
    MonotoneChainMethod()

This is an algorithm for the `convex_hull` function.

Uses [`DelaunayTriangulation.jl`](https://github.com/JuliaGeometry/DelaunayTriangulation.jl) to compute the convex hull.
This is a pure Julia algorithm which provides an optimal Delaunay triangulation.

See also `convex_hull`
"""
struct MonotoneChainMethod end

GrahamScanMethod, etc. can be implemented in GO as well, if someone wants to. If we add an extension on Quickhull.jl, then that would be another algorithm.

convex_hull(geometries) = convex_hull(MonotoneChainMethod(), geometries)

TODO: have this respect the CRS by pulling it out of geometries.

function convex_hull(::MonotoneChainMethod, geometries)

Extract all points as tuples. We have to collect and allocate here, because DelaunayTriangulation only accepts vectors of point-like geoms.

Cleanest would be to use the iterable from GO.flatten directly, but that would require us to implement the convex hull algorithm directly.

TODO: create a specialized method that extracts only the information required, GeometryBasics points can be passed through directly.

    points = collect(flatten(tuples, GI.PointTrait, geometries))

Compute the convex hull using DelTri (shorthand for DelaunayTriangulation.jl).

    hull = DelaunayTriangulation.convex_hull(points)

Convert the result to a GI.Polygon and return it. View would be more efficient here, but re-allocating is cleaner.

    point_vec = DelaunayTriangulation.get_points(hull)[DelaunayTriangulation.get_vertices(hull)]
    return GI.Polygon([GI.LinearRing(point_vec)])
end

---

This page was generated using Literate.jl.