GeometryOps.jl

Appearance

Simplify ​

GeometryOps.simplify Function
julia
simplify(obj; kw...)
simplify(::SimplifyAlg, obj; kw...)

Simplify a geometry, feature, feature collection, or nested vectors or a table of these.

RadialDistance, DouglasPeucker, or VisvalingamWhyatt algorithms are available, listed in order of increasing quality but decreasing performance.

PoinTrait and MultiPointTrait are returned unchanged.

The default behaviour is simplify(DouglasPeucker(; kw...), obj). Pass in other SimplifyAlg to use other algorithms.

Keywords

  • prefilter_alg: SimplifyAlg algorithm used to pre-filter object before using primary filtering algorithm.

  • threaded: true or false. Whether to use multithreading. Defaults to false.

  • crs: The CRS to attach to geometries. Defaults to nothing.

  • calc_extent: true or false. Whether to calculate the extent. Defaults to false.

Keywords for DouglasPeucker are allowed when no algorithm is specified:

Keywords

  • ratio: the fraction of points that should remain after simplify. Useful as it will generalise for large collections of objects.

  • number: the number of points that should remain after simplify. Less useful for large collections of mixed size objects.

  • tol: the minimum distance a point will be from the line joining its neighboring points.

Example

Simplify a polygon to have six points:

julia
import GeoInterface as GI
import GeometryOps as GO

poly = GI.Polygon([[
    [-70.603637, -33.399918],
    [-70.614624, -33.395332],
    [-70.639343, -33.392466],
    [-70.659942, -33.394759],
    [-70.683975, -33.404504],
    [-70.697021, -33.419406],
    [-70.701141, -33.434306],
    [-70.700454, -33.446339],
    [-70.694274, -33.458369],
    [-70.682601, -33.465816],
    [-70.668869, -33.472117],
    [-70.646209, -33.473835],
    [-70.624923, -33.472117],
    [-70.609817, -33.468107],
    [-70.595397, -33.458369],
    [-70.587158, -33.442901],
    [-70.587158, -33.426283],
    [-70.590591, -33.414248],
    [-70.594711, -33.406224],
    [-70.603637, -33.399918]]])

simple = GO.simplify(poly; number=6)
GI.npoint(simple)

# output
6
source
GeometryOps.VisvalingamWhyatt Type
julia
VisvalingamWhyatt <: SimplifyAlg

VisvalingamWhyatt(; kw...)

Simplifies geometries by removing points below tol distance from the line between its neighboring points.

Keywords

  • ratio: the fraction of points that should remain after simplify. Useful as it will generalise for large collections of objects.

  • number: the number of points that should remain after simplify. Less useful for large collections of mixed size objects.

  • tol: the minimum area of a triangle made with a point and its neighboring points.

Note: user input tol is doubled to avoid unnecessary computation in algorithm.

source
GeometryOps.DouglasPeucker Type
julia
DouglasPeucker <: SimplifyAlg

DouglasPeucker(; number, ratio, tol)

Simplifies geometries by removing points below tol distance from the line between its neighboring points.

Keywords

  • ratio: the fraction of points that should remain after simplify. Useful as it will generalise for large collections of objects.

  • number: the number of points that should remain after simplify. Less useful for large collections of mixed size objects.

  • tol: the minimum distance a point will be from the line joining its neighboring points.

Note: user input tol is squared to avoid unnecessary computation in algorithm.

source
GeometryOps.RadialDistance Type
julia
RadialDistance <: SimplifyAlg

Simplifies geometries by removing points less than tol distance from the line between its neighboring points.

Keywords

  • ratio: the fraction of points that should remain after simplify. Useful as it will generalise for large collections of objects.

  • number: the number of points that should remain after simplify. Less useful for large collections of mixed size objects.

  • tol: the minimum distance between points.

Note: user input tol is squared to avoid unnecessary computation in algorithm.

source

What is Geometry Simplification? ​

Geometry simplification reduces the number of points in a geometry while preserving its essential shape. This is usually done by specifying some tolerance.

GeometryOps provides three simplification algorithms: VisvalingamWhyatt, DouglasPeucker, and RadialDistance, listed in order of decreasing quality but increasing performance.

The default algorithm is DouglasPeucker, which is also available through the GEOS extension.

In GeometryOps' algorithms, you can specify tol, number of points, or ratio of points after simplification to points in the input geometry.

The GEOS extension (activated by loading LibGEOS.jl) also allows for GEOS's topology preserving simplification as well as Douglas-Peucker simplification implemented in GEOS. Call this by passing GEOS(; method = :TopologyPreserve) or GEOS(; method = :DouglasPeucker) to the algorithm.

Examples ​

Here is the simplest example:

julia
using Makie, GeoInterfaceMakie
import GeoInterface as GI
import GeometryOps as GO

original = GI.Polygon([[[-70.603637, -33.399918], [-70.614624, -33.395332], [-70.639343, -33.392466], [-70.659942, -33.394759], [-70.683975, -33.404504], [-70.697021, -33.419406], [-70.701141, -33.434306], [-70.700454, -33.446339], [-70.694274, -33.458369], [-70.682601, -33.465816], [-70.668869, -33.472117], [-70.646209, -33.473835], [-70.624923, -33.472117], [-70.609817, -33.468107], [-70.595397, -33.458369], [-70.587158, -33.442901], [-70.587158, -33.426283], [-70.590591, -33.414248], [-70.594711, -33.406224], [-70.603637, -33.399918]]])

simple = GO.simplify(original; number=6)

f, a, p = poly(original; label = "Original")
poly!(simple; label = "Simplified")
axislegend(a)
f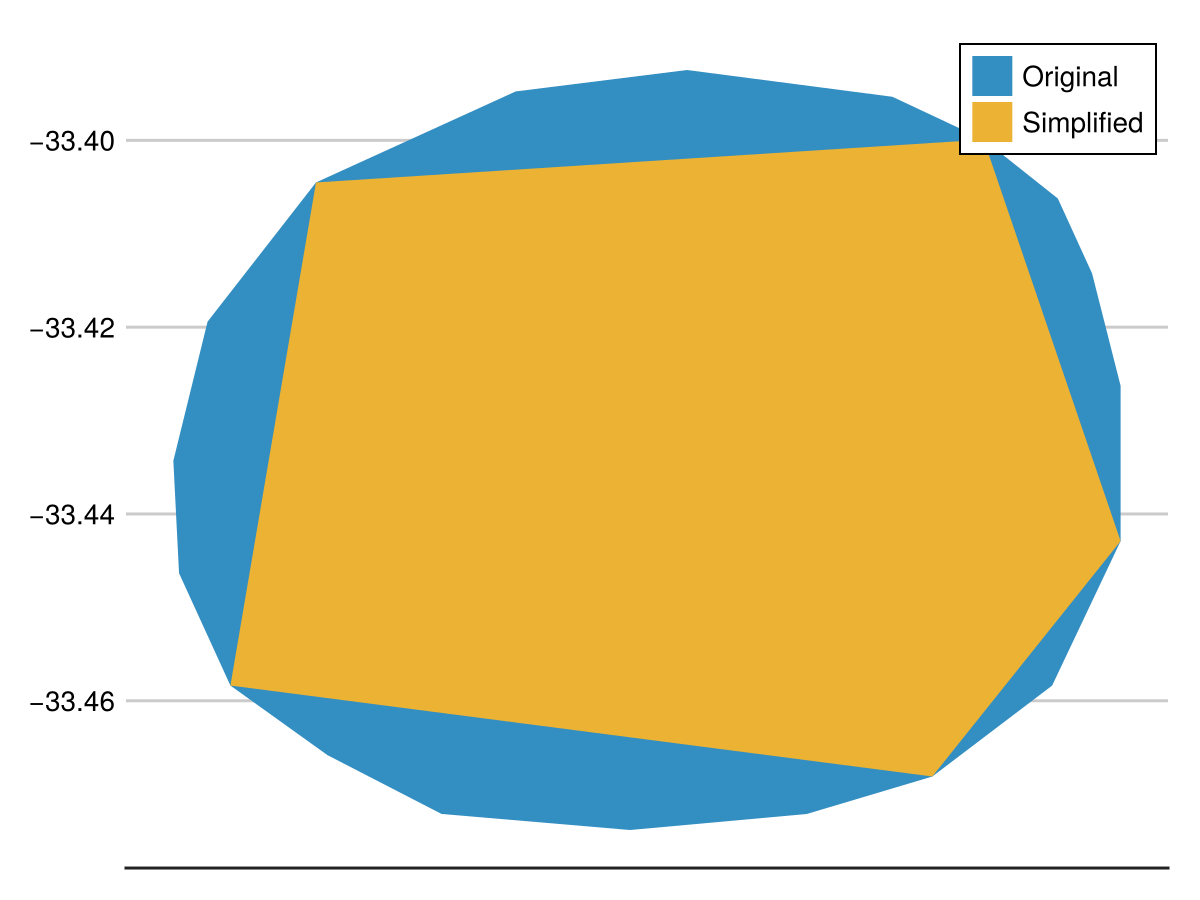

You can also choose the algorithm to use. The algorithm we run here is the same as what we used above:

julia
GO.simplify(GO.DouglasPeucker(number = 6), original)
GeoInterface.Wrappers.Polygon{false, false}([GeoInterface.Wrappers.LinearRing([(-70.603637, -33.399918), … (4) … , (-70.603637, -33.399918)])])

Benchmarks ​

Let's benchmark the performance of the algorithms to get a clearer idea of what's going on.

TODO: I had benchmarks but they were not particularly useful. We need to make them better.

julia
export simplify, VisvalingamWhyatt, DouglasPeucker, RadialDistance

const _SIMPLIFY_TARGET = TraitTarget{Union{GI.PolygonTrait, GI.AbstractCurveTrait, GI.MultiPointTrait, GI.PointTrait}}()
const MIN_POINTS = 3
const SIMPLIFY_ALG_KEYWORDS = """
# Keywords

- `ratio`: the fraction of points that should remain after `simplify`.
    Useful as it will generalise for large collections of objects.
- `number`: the number of points that should remain after `simplify`.
    Less useful for large collections of mixed size objects.
"""
const DOUGLAS_PEUCKER_KEYWORDS = """
$SIMPLIFY_ALG_KEYWORDS
- `tol`: the minimum distance a point will be from the line
    joining its neighboring points.
"""

"""
    abstract type SimplifyAlg

Abstract type for simplification algorithms.

# API

For now, the algorithm must hold the `number`, `ratio` and `tol` properties.

Simplification algorithm types can hook into the interface by implementing
the `_simplify(trait, alg, geom)` methods for whichever traits are necessary.
"""
abstract type SimplifyAlg end

"""
    simplify(obj; kw...)
    simplify(::SimplifyAlg, obj; kw...)

Simplify a geometry, feature, feature collection,
or nested vectors or a table of these.

`RadialDistance`, `DouglasPeucker`, or
`VisvalingamWhyatt` algorithms are available,
listed in order of increasing quality but decreasing performance.

`PoinTrait` and `MultiPointTrait` are returned unchanged.

The default behaviour is `simplify(DouglasPeucker(; kw...), obj)`.
Pass in other `SimplifyAlg` to use other algorithms.

Keywords

julia
- `prefilter_alg`: `SimplifyAlg` algorithm used to pre-filter object before
    using primary filtering algorithm.
$APPLY_KEYWORDS


Keywords for DouglasPeucker are allowed when no algorithm is specified:

$DOUGLAS_PEUCKER_KEYWORDS

Example

julia
Simplify a polygon to have six points:

```jldoctest
import GeoInterface as GI
import GeometryOps as GO

poly = GI.Polygon([[
    [-70.603637, -33.399918],
    [-70.614624, -33.395332],
    [-70.639343, -33.392466],
    [-70.659942, -33.394759],
    [-70.683975, -33.404504],
    [-70.697021, -33.419406],
    [-70.701141, -33.434306],
    [-70.700454, -33.446339],
    [-70.694274, -33.458369],
    [-70.682601, -33.465816],
    [-70.668869, -33.472117],
    [-70.646209, -33.473835],
    [-70.624923, -33.472117],
    [-70.609817, -33.468107],
    [-70.595397, -33.458369],
    [-70.587158, -33.442901],
    [-70.587158, -33.426283],
    [-70.590591, -33.414248],
    [-70.594711, -33.406224],
    [-70.603637, -33.399918]]])

simple = GO.simplify(poly; number=6)
GI.npoint(simple)

output

julia
6
```
"""
simplify(alg::SimplifyAlg, data; kw...) = _simplify(alg, data; kw...)
simplify(alg::GEOS, data; kw...) = _simplify(alg, data; kw...)

Default algorithm is DouglasPeucker

julia
simplify(
    data; prefilter_alg = nothing,
    calc_extent=false, threaded=false, crs=nothing, kw...,
 ) = _simplify(DouglasPeucker(; kw...), data; prefilter_alg, calc_extent, threaded, crs)


#= For each algorithm, apply simplification to all curves, multipoints, and
points, reconstructing everything else around them. =#
function _simplify(alg::Union{SimplifyAlg, GEOS}, data; prefilter_alg=nothing, kw...)
    simplifier(trait, geom) = _simplify(trait, alg, geom; prefilter_alg)
    return apply(WithTrait(simplifier), _SIMPLIFY_TARGET, data; kw...)
end


# For Point and MultiPoint traits we do nothing
_simplify(::GI.PointTrait, alg, geom; kw...) = geom
_simplify(::GI.MultiPointTrait, alg, geom; kw...) = geom

# For curves, rings, and polygon we simplify
function _simplify(
    ::GI.AbstractCurveTrait, alg, geom;
    prefilter_alg, preserve_endpoint = true,
)
    points = if isnothing(prefilter_alg)
        tuple_points(geom)
    else
        _simplify(prefilter_alg, tuple_points(geom), preserve_endpoint)
    end
    return rebuild(geom, _simplify(alg, points, preserve_endpoint))
end

function _simplify(::GI.PolygonTrait, alg, geom;  kw...)
    # Force treating children as LinearRing
    simplifier(g) = _simplify(
        GI.LinearRingTrait(), alg, g;
        kw..., preserve_endpoint = false,
    )
    lrs = map(simplifier, GI.getgeom(geom))
    return rebuild(geom, lrs)
end

Simplify with RadialDistance Algorithm ​

julia
"""
    RadialDistance <: SimplifyAlg

Simplifies geometries by removing points less than
`tol` distance from the line between its neighboring points.

$SIMPLIFY_ALG_KEYWORDS
- `tol`: the minimum distance between points.

Note: user input `tol` is squared to avoid unnecessary computation in algorithm.
"""
@kwdef struct RadialDistance <: SimplifyAlg
    number::Union{Int64,Nothing} = nothing
    ratio::Union{Float64,Nothing} = nothing
    tol::Union{Float64,Nothing} = nothing

    function RadialDistance(number, ratio, tol)
        _checkargs(number, ratio, tol)

square tolerance for reduced computation

julia
        tol = isnothing(tol) ? tol : tol^2
        new(number, ratio, tol)
    end
end

function _simplify(alg::RadialDistance, points::Vector, _)
    previous = first(points)
    distances = Array{Float64}(undef, length(points))
    for i in eachindex(points)
        point = points[i]
        distances[i] = _squared_euclid_distance(Float64, point, previous)
        previous = point
    end
    # Never remove the end points
    distances[begin] = distances[end] = Inf
    return _get_points(alg, points, distances)
end

Simplify with DouglasPeucker Algorithm ​

julia
"""
    DouglasPeucker <: SimplifyAlg

    DouglasPeucker(; number, ratio, tol)

Simplifies geometries by removing points below `tol`
distance from the line between its neighboring points.

$DOUGLAS_PEUCKER_KEYWORDS
Note: user input `tol` is squared to avoid unnecessary computation in algorithm.
"""
@kwdef struct DouglasPeucker <: SimplifyAlg
    number::Union{Int64,Nothing} = nothing
    ratio::Union{Float64,Nothing} = nothing
    tol::Union{Float64,Nothing} = nothing

    function DouglasPeucker(number, ratio, tol)
        _checkargs(number, ratio, tol)

square tolerance for reduced computation

julia
        tol = isnothing(tol) ? tol : tol^2
        return new(number, ratio, tol)
    end
end

#= Simplify using the DouglasPeucker algorithm - nice gif of process on wikipedia:
(https://en.wikipedia.org/wiki/Ramer-Douglas-Peucker_algorithm). =#
function _simplify(alg::DouglasPeucker, points::Vector, preserve_endpoint)
    npoints = length(points)
    npoints <= MIN_POINTS && return points

Determine stopping criteria

julia
    max_points = if !isnothing(alg.tol)
        npoints
    else
        npts = !isnothing(alg.number) ? alg.number : max(3, round(Int, alg.ratio * npoints))
        npts ≥ npoints && return points
        npts
    end
    max_tol = !isnothing(alg.tol) ? alg.tol : zero(Float64)

Set up queue

julia
    queue = Vector{Tuple{Int, Int, Int, Float64}}()
    queue_idx, queue_dist = 0, zero(Float64)
    len_queue = 0

Set up results vector

julia
    results = Vector{Int}(undef, max_points + (preserve_endpoint ? 0 : 1))
    results[1], results[2] = 1, npoints

Loop through points until stopping criteria are fulfilled

julia
    i = 2  # already have first and last point added
    start_idx, end_idx = 1, npoints
    max_idx, max_dist = _find_max_squared_dist(points, start_idx, end_idx)
    while i ≤ min(MIN_POINTS + 1, max_points) || (i < max_points && max_dist > max_tol)

Add next point to results

julia
        i += 1
        results[i] = max_idx

Determine which point to add next by checking left and right of point

julia
        left_idx, left_dist = _find_max_squared_dist(points, start_idx, max_idx)
        right_idx, right_dist = _find_max_squared_dist(points, max_idx, end_idx)
        left_vals = (start_idx, left_idx, max_idx, left_dist)
        right_vals = (max_idx, right_idx, end_idx, right_dist)

Add and remove values from queue

julia
        if queue_dist > left_dist && queue_dist > right_dist

Value in queue is next value to add to results

julia
            start_idx, max_idx, end_idx, max_dist = queue[queue_idx]

Add left and/or right values to queue or delete used queue value

julia
            if left_dist > 0
                queue[queue_idx] = left_vals
                if right_dist > 0
                    push!(queue, right_vals)
                    len_queue += 1
                end
            elseif right_dist > 0
                queue[queue_idx] = right_vals
            else
                deleteat!(queue, queue_idx)
                len_queue -= 1
            end

Determine new maximum queue value

julia
            queue_dist, queue_idx = !isempty(queue) ?
                findmax(x -> x[4], queue) : (zero(Float64), 0)
        elseif left_dist > right_dist  # use left value as next value to add to results
            push!(queue, right_vals)  # add right value to queue
            len_queue += 1
            if right_dist > queue_dist
                queue_dist = right_dist
                queue_idx = len_queue
            end
            start_idx, max_idx, end_idx, max_dist = left_vals
        else  # use right value as next value to add to results
            push!(queue, left_vals)  # add left value to queue
            len_queue += 1
            if left_dist > queue_dist
                queue_dist = left_dist
                queue_idx = len_queue
            end
            start_idx, max_idx, end_idx, max_dist = right_vals
        end
    end
    sorted_results = sort!(@view results[1:i])
    if !preserve_endpoint && i > 3

Check start/endpoint distance to other points to see if it meets criteria

julia
        pre_pt, post_pt = points[sorted_results[end - 1]], points[sorted_results[2]]
        endpt_dist = _squared_distance_line(Float64, points[1], pre_pt, post_pt)
        if !isnothing(alg.tol)

Remove start point and replace with second point

julia
            if endpt_dist < max_tol
                results[i] = results[2]
                sorted_results = @view results[2:i]
            end
        else

Remove start point and add point with maximum distance still remaining

julia
            if endpt_dist < max_dist
                insert!(results, searchsortedfirst(sorted_results, max_idx), max_idx)
                results[i+1] = results[2]
                sorted_results = @view results[2:i+1]
            end
        end
    end
    return points[sorted_results]
end

#= find maximum distance of any point between the start_idx and end_idx to the line formed
by connecting the points at start_idx and end_idx. Note that the first index of maximum
value will be used, which might cause differences in results from other algorithms.=#
function _find_max_squared_dist(points, start_idx, end_idx)
    max_idx = start_idx
    max_dist = zero(Float64)
    for i in (start_idx + 1):(end_idx - 1)
        d = _squared_distance_line(Float64, points[i], points[start_idx], points[end_idx])
        if d > max_dist
            max_dist = d
            max_idx = i
        end
    end
    return max_idx, max_dist
end

Simplify with VisvalingamWhyatt Algorithm ​

julia
"""
    VisvalingamWhyatt <: SimplifyAlg

    VisvalingamWhyatt(; kw...)

Simplifies geometries by removing points below `tol`
distance from the line between its neighboring points.

$SIMPLIFY_ALG_KEYWORDS
- `tol`: the minimum area of a triangle made with a point and
    its neighboring points.
Note: user input `tol` is doubled to avoid unnecessary computation in algorithm.
"""
@kwdef struct VisvalingamWhyatt <: SimplifyAlg
    number::Union{Int,Nothing} = nothing
    ratio::Union{Float64,Nothing} = nothing
    tol::Union{Float64,Nothing} = nothing

    function VisvalingamWhyatt(number, ratio, tol)
        _checkargs(number, ratio, tol)

double tolerance for reduced computation

julia
        tol = isnothing(tol) ? tol : tol*2
        return new(number, ratio, tol)
    end
end

function _simplify(alg::VisvalingamWhyatt, points::Vector, _)
    length(points) <= MIN_POINTS && return points
    areas = _build_tolerances(_triangle_double_area, points)
    return _get_points(alg, points, areas)
end

Calculates double the area of a triangle given its vertices

julia
_triangle_double_area(p1, p2, p3) =
    abs(p1[1] * (p2[2] - p3[2]) + p2[1] * (p3[2] - p1[2]) + p3[1] * (p1[2] - p2[2]))

Shared utils ​

julia
function _build_tolerances(f, points)
    nmax = length(points)
    real_tolerances = _flat_tolerances(f, points)

    tolerances = copy(real_tolerances)
    i = [n for n in 1:nmax]

    this_tolerance, min_vert = findmin(tolerances)
    _remove!(tolerances, min_vert)
    deleteat!(i, min_vert)

    while this_tolerance < Inf
        skip = false

        if min_vert < length(i)
            right_tolerance = f(
                points[i[min_vert - 1]],
                points[i[min_vert]],
                points[i[min_vert + 1]],
            )
            if right_tolerance <= this_tolerance
                right_tolerance = this_tolerance
                skip = min_vert == 1
            end

            real_tolerances[i[min_vert]] = right_tolerance
            tolerances[min_vert] = right_tolerance
        end

        if min_vert > 2
            left_tolerance = f(
                points[i[min_vert - 2]],
                points[i[min_vert - 1]],
                points[i[min_vert]],
            )
            if left_tolerance <= this_tolerance
                left_tolerance = this_tolerance
                skip = min_vert == 2
            end
            real_tolerances[i[min_vert - 1]] = left_tolerance
            tolerances[min_vert - 1] = left_tolerance
        end

        if !skip
            min_vert = argmin(tolerances)
        end
        deleteat!(i, min_vert)
        this_tolerance = tolerances[min_vert]
        _remove!(tolerances, min_vert)
    end

    return real_tolerances
end

function tuple_points(geom)
    points = Array{Tuple{Float64,Float64}}(undef, GI.npoint(geom))
    for (i, p) in enumerate(GI.getpoint(geom))
        points[i] = (GI.x(p), GI.y(p))
    end
    return points
end

function _get_points(alg, points, tolerances)
    # This assumes that `alg` has the properties
    # `tol`, `number`, and `ratio` available...
    tol = alg.tol
    number = alg.number
    ratio = alg.ratio
    bit_indices = if !isnothing(tol)
        _tol_indices(alg.tol::Float64, points, tolerances)
    elseif !isnothing(number)
        _number_indices(alg.number::Int64, points, tolerances)
    else
        _ratio_indices(alg.ratio::Float64, points, tolerances)
    end
    return points[bit_indices]
end

function _tol_indices(tol, points, tolerances)
    tolerances .>= tol
end

function _number_indices(n, points, tolerances)
    tol = partialsort(tolerances, length(points) - n + 1)
    bit_indices = _tol_indices(tol, points, tolerances)
    nselected = sum(bit_indices)
    # If there are multiple values exactly at `tol` we will get
    # the wrong output length. So we need to remove some.
    while nselected > n
        min_tol = Inf
        min_i = 0
        for i in eachindex(bit_indices)
            bit_indices[i] || continue
            if tolerances[i] < min_tol
                min_tol = tolerances[i]
                min_i = i
            end
        end
        nselected -= 1
        bit_indices[min_i] = false
    end
    return bit_indices
end

function _ratio_indices(r, points, tolerances)
    n = max(3, round(Int, r * length(points)))
    return _number_indices(n, points, tolerances)
end

function _flat_tolerances(f, points)::Vector{Float64}
    result = Vector{Float64}(undef, length(points))
    result[1] = result[end] = Inf

    for i in 2:length(result) - 1
        result[i] = f(points[i-1], points[i], points[i+1])
    end
    return result
end

function _remove!(s, i)
    for j in i:lastindex(s)-1
        s[j] = s[j+1]
    end
end

Check SimplifyAlgs inputs to make sure they are valid for below algorithms

julia
function _checkargs(number, ratio, tol)
    count(isnothing, (number, ratio, tol)) == 2 ||
        error("Must provide one of `number`, `ratio` or `tol` keywords")
    if !isnothing(number)
        if number < MIN_POINTS
            error("`number` must be $MIN_POINTS or larger. Got $number")
        end
    elseif !isnothing(ratio)
        if ratio <= 0 || ratio > 1
            error("`ratio` must be 0 < ratio <= 1. Got $ratio")
        end
    else  # !isnothing(tol)
        if tol ≤ 0
            error("`tol` must be a positive number. Got $tol")
        end
    end
    return nothing
end

This page was generated using Literate.jl.