Voronoi Tessellation

The Voronoi tessellation of a set of points is a partitioning of the plane into regions based on distance to points. Each region contains all points closer to one generator point than to any other.

GeometryOps.jl provides a method for computing the Voronoi tessellation of a set of points, using the DelaunayTriangulation.jl package.

Right now, the GeometryOps.jl method can only provide clipped voronoi tesselations, as the function returns a list of GeoInterface polygons. If you need an unbounded tessellation, open an issue and we can discuss the best way to represent unbounded polygons within GeometryOps.

Example

Simple tessellation

import GeometryOps as GO, GeoInterface as GI
using CairoMakie # to plot

points = tuple.(randn(20), randn(20))
polygons = GO.voronoi(points)
f, a, p = plot(polygons[1]; label = "Voronoi cell 1")
for (i, poly) in enumerate(polygons[2:end])
    plot!(a, poly; label = "Voronoi cell $(i+1)")
end
scatter!(a, points; color = :black, markersize = 10, label = "Generators")
axislegend(a)
f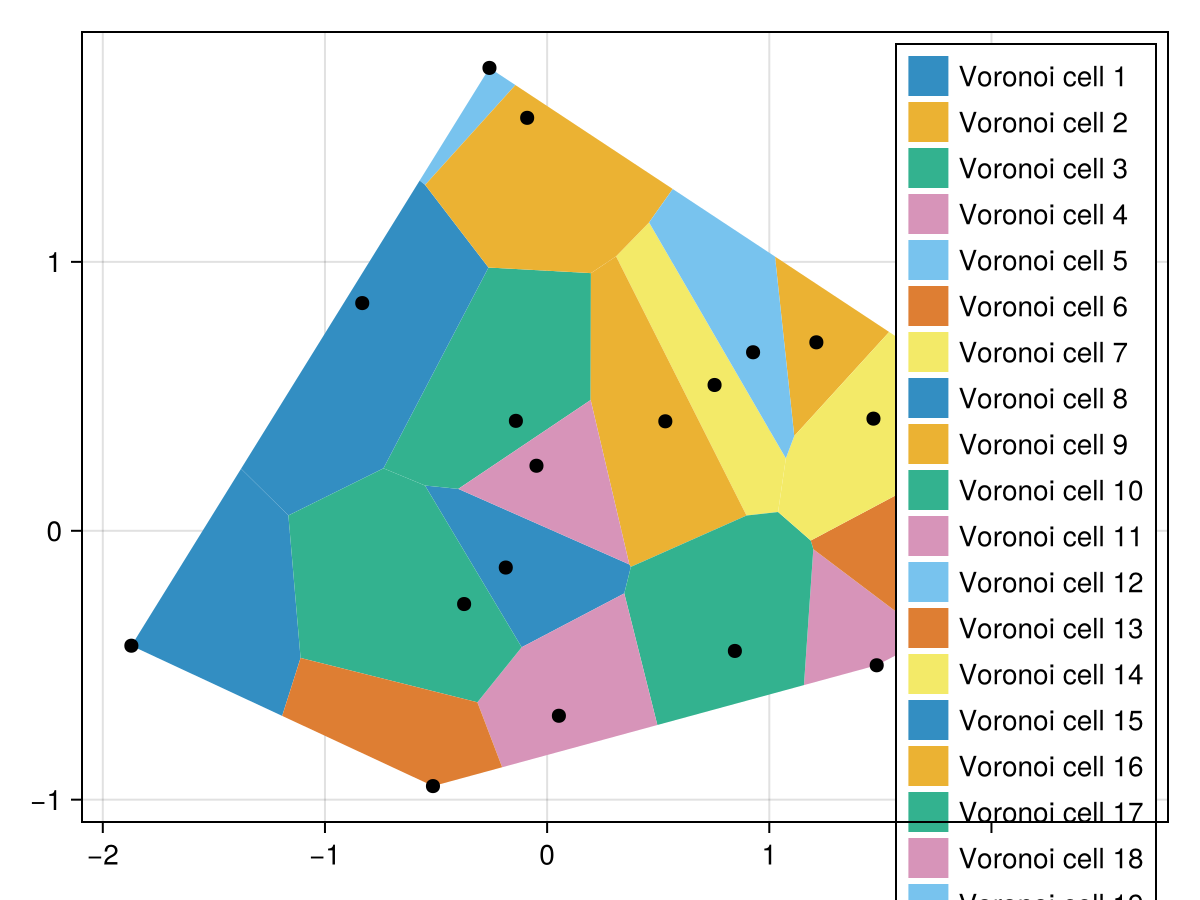

Implementation

This implementation mainly just preforms some assertion checks before passing the Arguments to the DelaunayTriangulation package. We always set the argument clip to the DelaunayTriangulation voronoi call to True such that we can return a list of valid polygons. The default clipping polygon is the convex hull of the tessleation, but the user can pass in a bounding polygon with the clip_polygon argument. After the call to voronoi, the call then unpacks the voronoi output into GeoInterface polygons, whose point match the float type input by the user.

struct __NoCRSProvided end

"""
    voronoi(geometries, [T = Float64]; clip_polygon = nothing, kwargs...)

Compute the Voronoi tessellation of the points in `geometries`.
Returns a vector of `GI.Polygon` objects representing the Voronoi cells,
in the same order as the input points.

# Arguments
- `geometries`: Any GeoInterface-compatible geometry or collection of geometries
  that can be decomposed into points
- `T`: Float-type for returned polygons points (default: Float64)

# Keyword Arguments
- `clip_polygon`: what bounding shape should the Voronoi cells be clipped to? (default: nothing -> clipped to the convex hull)
    clip_polygon can of several types: (1) a GeoInterface polygon, (2) a two-element tuple where the first element is a list of tuple points
    and the second element is a list of integer indices to indicate the order of the provided points, or (3) a a two-element tuple where the
    first element is a tuple of tuple points and the second element is a tuple of integer indices to indicate the order of the provided points
- $CRS_KEYWORD
- `rng`: random number generator to generating the voronoi tesselation

!!! warning
    This interface only computes the 2-dimensional Voronoi tessellation!
    Only clipped voronoi tesselations can be created!
    Only `T = Float64` or `Float32` are guaranteed good results by the underlying package DelaunayTriangulation.

!!! note
    The polygons are returned in the same order as the input points after flattening.
    Each polygon corresponds to the Voronoi cell of the point at the same index.

# Examples
An example with default clipping to the convex hull.

```jldoctest voronoi
import GeometryOps as GO
import GeoInterface as GI
using Random

rng = Xoshiro(0)
points = [(rand(rng), rand(rng)) .* 5 for i in range(1, 3)]
GO.voronoi(points; rng = rng)

output

3-element Vector{GeoInterface.Wrappers.Polygon{false, false, Vector{GeoInterface.Wrappers.LinearRing{false, false, Vector{Tuple{Float64, Float64}}, Nothing, Nothing}}, Nothing, Nothing}}:
 GeoInterface.Wrappers.Polygon{false, false}([GeoInterface.Wrappers.LinearRing([(4.310704285977424, 0.42985432929210976), … (2) … , (4.310704285977424, 0.42985432929210976)])])
 GeoInterface.Wrappers.Polygon{false, false}([GeoInterface.Wrappers.LinearRing([(3.7949144210695653, 0.4101636087384888), … (4) … , (3.7949144210695653, 0.4101636087384888)])])
 GeoInterface.Wrappers.Polygon{false, false}([GeoInterface.Wrappers.LinearRing([(2.685897788908803, 0.3678259474564151), … (2) … , (2.685897788908803, 0.3678259474564151)])])
```

An example with clipping to a GeoInterface polygon.
```jldoctest voronoi
clip_points = ((0.0,0.0), (5.0,0.0), (5.0,5.0), (0.0,5.0), (0.0,0.0))
clip_order = (1, 2, 3, 4, 1)
clip_poly1 = GI.Polygon([collect(clip_points)])
GO.voronoi(points; clip_polygon = clip_poly1, rng = rng)

output

3-element Vector{GeoInterface.Wrappers.Polygon{false, false, Vector{GeoInterface.Wrappers.LinearRing{false, false, Vector{Tuple{Float64, Float64}}, Nothing, Nothing}}, Nothing, Nothing}}:
 GeoInterface.Wrappers.Polygon{false, false}([GeoInterface.Wrappers.LinearRing([(5.0, 0.0), … (3) … , (5.0, 0.0)])])
 GeoInterface.Wrappers.Polygon{false, false}([GeoInterface.Wrappers.LinearRing([(3.7328227614527916, 0.0), … (3) … , (3.7328227614527916, 0.0)])])
 GeoInterface.Wrappers.Polygon{false, false}([GeoInterface.Wrappers.LinearRing([(0.0, 5.0), … (3) … , (0.0, 5.0)])])
```

An example with clipping to a tuple of tuples.
```jldoctest voronoi
clip_poly2 = (clip_points, clip_order) # tuples
GO.voronoi(points; clip_polygon = clip_poly2, rng = rng)

output

3-element Vector{GeoInterface.Wrappers.Polygon{false, false, Vector{GeoInterface.Wrappers.LinearRing{false, false, Vector{Tuple{Float64, Float64}}, Nothing, Nothing}}, Nothing, Nothing}}:
 GeoInterface.Wrappers.Polygon{false, false}([GeoInterface.Wrappers.LinearRing([(5.0, 0.0), … (3) … , (5.0, 0.0)])])
 GeoInterface.Wrappers.Polygon{false, false}([GeoInterface.Wrappers.LinearRing([(3.7328227614527916, 0.0), … (3) … , (3.7328227614527916, 0.0)])])
 GeoInterface.Wrappers.Polygon{false, false}([GeoInterface.Wrappers.LinearRing([(0.0, 5.0), … (3) … , (0.0, 5.0)])])
```

An example with clipping to a tuple of vectors.
```jldoctest voronoi
clip_poly3 = (collect(clip_points), collect(clip_order)) # vectors
GO.voronoi(points; clip_polygon = clip_poly3, rng = rng)

output

3-element Vector{GeoInterface.Wrappers.Polygon{false, false, Vector{GeoInterface.Wrappers.LinearRing{false, false, Vector{Tuple{Float64, Float64}}, Nothing, Nothing}}, Nothing, Nothing}}:
 GeoInterface.Wrappers.Polygon{false, false}([GeoInterface.Wrappers.LinearRing([(5.0, 0.0), … (3) … , (5.0, 0.0)])])
 GeoInterface.Wrappers.Polygon{false, false}([GeoInterface.Wrappers.LinearRing([(3.7328227614527916, 0.0), … (3) … , (3.7328227614527916, 0.0)])])
 GeoInterface.Wrappers.Polygon{false, false}([GeoInterface.Wrappers.LinearRing([(0.0, 5.0), … (3) … , (0.0, 5.0)])])
```

"""
function voronoi(geometries, ::Type{T} = Float64; kwargs...) where T
    return voronoi(Planar(), geometries, T; kwargs...)
end

function voronoi(::Planar, geometries, ::Type{T} = Float64; clip_polygon = nothing, crs = __NoCRSProvided(), kwargs...) where T

Extract all points as tuples using GO.flatten This handles any GeoInterface-compatible input

    points_iter = collect(flatten(tuples, GI.PointTrait, geometries))
    if crs isa __NoCRSProvided
        crs = GI.crs(geometries)
    end

if we have not figured it out yet, we can't do anything

    if crs isa __NoCRSProvided
        error("This code should be unreachable; please file an issue at https://github.com/JuliaGeometry/GeometryOps.jl/issues with the stacktrace and a reproducible example.")
    end

Handle edge case of too few points

    if length(points_iter) < 3
        throw(ArgumentError("Voronoi tessellation requires at least 3 points, got $(length(points_iter))"))
    end

Compute Delaunay triangulation

    tri = DelTri.triangulate(points_iter; kwargs...)

Compute Voronoi tessellation from the triangulation

    _clip_polygon = if isnothing(clip_polygon)
        nothing
    elseif GI.geomtrait(clip_polygon) isa GI.PolygonTrait
        _clean_voronoi_clip_polygon_inputs(clip_polygon)
    else
        _clean_voronoi_clip_point_inputs(clip_polygon)
    end

if isclockwise(clip_polygon)

    vorn = DelTri.voronoi(tri; clip = true, clip_polygon = _clip_polygon)

    polygons = GeoInterface.Wrappers.Polygon{false, false, Vector{GeoInterface.Wrappers.LinearRing{false, false, Vector{Tuple{T, T}}, Nothing, Nothing}}, Nothing, typeof(crs)}[]
    sizehint!(polygons, DelTri.num_polygons(vorn))

Implementation below copied from Makie.jl see https://github.com/MakieOrg/Makie.jl/blob/687c4466ce00154714297e36a7f610443c6ad5be/Makie/src/basic_recipes/voronoiplot.jl#L101-L110

    for i in DelTri.each_generator(vorn)
        !DelTri.has_polygon(vorn, i) && continue
        polygon_coords = DelTri.getxy.(DelTri.get_polygon_coordinates(vorn, i))
        push!(polygons, GI.Polygon([GI.LinearRing(polygon_coords)], crs = crs))

The code below gets the generator point, but we don't need it gp = DelTri.getxy(DelTri.get_generator(vorn, i)) !isempty(polygon_coords) && push!(generators, gp)

    end

    return polygons
end

function _clean_voronoi_clip_polygon_inputs(clip_polygon)
    @assert GI.nhole(clip_polygon) == 0
    points = collect(flatten(tuples, GI.PointTrait, clip_polygon))
    npoints = GI.npoint(clip_polygon)
    if points[1] == points[end]
        npoints -= 1
        points = points[1:npoints]
    end
    point_order = collect(1:npoints)
    return _clean_voronoi_clip_point_inputs((points, point_order))
end

function _clean_voronoi_clip_point_inputs((points, point_order)::Tuple{Vector{<:Tuple{<:Any, <:Any}}, Vector{<:Integer}})
    combined_data = collect(zip(points, point_order))
    sort!(combined_data, by = last)
    unique!(combined_data)

    points, point_order = first.(combined_data), last.(combined_data)
    push!(points, points[1])
    push!(point_order, 1)

    if isclockwise(GI.LineString(points))
        reverse!(points)
    end
    return points, point_order
end

_clean_voronoi_clip_point_inputs((points, point_order)::Tuple{NTuple{<:Any, <:Tuple{<:Any, <:Any}}, NTuple{<:Any, <:Integer}}) =
    _clean_voronoi_clip_point_inputs((collect(points), collect(point_order)))

function _clean_voronoi_clip_point_inputs(clip_polygon)
    error("Clip polygon must be a polygon or other recognizable form, see the docstring for `DelaunayTriangulation.voronoi` for the recognizable form.  Was neither, got $(typeof(clip_polygon))")
    return
end

---

This page was generated using Literate.jl.