Smooth

Geometry smoothing is meant to make shapes more aesthetically pleasing, usually by rounding out rough edges and corners.

You can do this by the smooth function, which uses the Chaikin algorithm by default.

Example

using CairoMakie
import GeoInterface as GI, GeometryOps as GO

line = GI.LineString([(0.0, 0.0), (1.0, 1.0), (2.0, 0.0)])
smoothed = GO.smooth(line)
smoothed_2 = GO.smooth(line; iterations=2)

f, a, p = lines(line; label = "Original")
lines!(a, smoothed; label = "1 iteration")
lines!(a, smoothed_2; label = "2 iterations")
axislegend(a)
f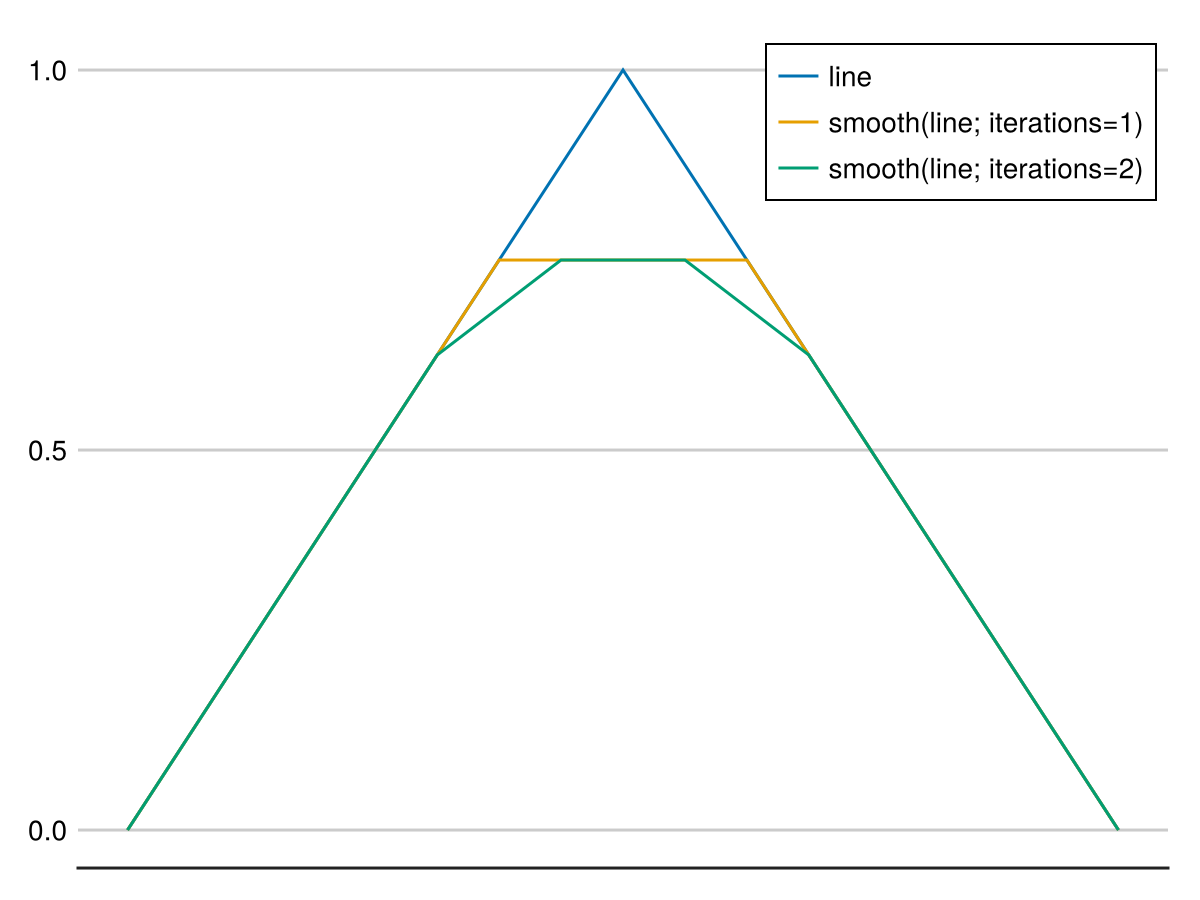ig

Smoothing also works on the Spherical manifold, similarly to the planar manifold (default):

using CairoMakie
import GeoInterface as GI, GeometryOps as GO

line = GI.LineString([(0.0, 0.0), (1.0, 1.0), (2.0, 0.0)])
smoothed = GO.smooth(GO.Spherical(), line) |> x -> GO.transform(GO.UnitSpherical.GeographicFromUnitSpherical(), x)
smoothed_2 = GO.smooth(GO.Spherical(), line; iterations=2) |> x -> GO.transform(GO.UnitSpherical.GeographicFromUnitSpherical(), x)

f, a, p = lines(line; label = "Original", axis = (; title = "Spherical smoothing"))
lines!(a, smoothed; label = "1 iteration")
lines!(a, smoothed_2; label = "2 iterations")
axislegend(a)
fig

"""
    Chaikin(; iterations=1, manifold=Planar())

Smooths geometries using Chaikin's corner-cutting algorithm [^1].
This algorithm "slices" off every corner of the geometry to smooth it out,
equivalent to a sequence of quadratic Bezier curves.

# Keywords
- `iterations`: the number of times to apply the algorithm.
- `manifold`: the `Manifold` to smooth the geometry on.  Currently, `Planar` and `Spherical` are supported.

Extended help

The algorithm is very simple; for each corner of the line (a -> b -> c),
insert two new points and remove b, such that `a -> b -> c` becomes
`a -> q -> r -> c`, where `q` and `r` are the new points such that:

```math
q = 3/4 * b + 1/4 * a
r = 3/4 * b + 1/4 * c
```

In practice the replacement happens on the level of each edge.

# References
[^1]: Chaikin, G. An algorithm for high speed curve generation. Computer Graphics and Image Processing 3 (1974), 346-349
"""
@kwdef struct Chaikin{M} <: Algorithm{M}
    manifold::M = Planar()
    iterations::Int = 1
end

"""
    smooth(alg::Algorithm, geom)
    smooth(geom; kw...)

Smooths a geometry using the provided algorithm.

The default algorithm is `Chaikin()`, which can be used on the spherical or planar manifolds.
"""
smooth(geom; kw...) = smooth(Chaikin(; kw...), geom)
smooth(m::Manifold, geom; kw...) = smooth(Chaikin(; manifold=m, kw...), geom)
function smooth(alg::Algorithm, geom; kw...)
    _smooth_function(trait, geom) = _smooth(alg, trait, geom)
    return apply(
        WithTrait(_smooth_function),
        TraitTarget{Union{GI.AbstractCurveTrait,GI.MultiPointTrait,GI.PointTrait}}(),
        geom;
        kw...
    )
end

_smooth(alg, ::GI.PointTrait, geom) = geom
_smooth(alg, ::GI.MultiPointTrait, geom) = geom

function _smooth(alg::Chaikin{<: Planar}, trait::Trait, geom) where {M, Trait <: Union{GI.LineStringTrait,GI.LinearRingTrait}}
    isring = Trait <: GI.LinearRingTrait
    points = tuple_points(geom)
    if isring && first(points) != last(points)
        push!(points, first(points))
    end
    smoothed_points = _chaikin_smooth(alg.manifold, points, alg.iterations, isring)
    return rebuild(geom, smoothed_points)
end

function _smooth(alg::Chaikin{<: M}, trait::Trait, geom) where {M <: Spherical, Trait <: Union{GI.LineStringTrait,GI.LinearRingTrait}}
    isring = Trait <: GI.LinearRingTrait
    points = apply(UnitSphereFromGeographic(), GI.PointTrait(), geom).geom
    if isring && first(points) != last(points)
        push!(points, first(points))
    end
    smoothed_points = _chaikin_smooth(alg.manifold, points, alg.iterations, isring)
    return rebuild(geom, smoothed_points)
end

function _chaikin_smooth(manifold::M, points::Vector{P}, iterations::Int, isring::Bool) where {M <: Manifold, P}

points is expected to be a vector of points

    smoothed_points = points
    for itr in 1:iterations
        num_points = length(smoothed_points)
        if isring
            n = 1
            new_points = Vector{P}(undef, num_points * 2 - 1)
        else
            n = 2

Need to add the first point

            new_points = Vector{P}(undef, num_points * 2)
            new_points[begin] = smoothed_points[begin]
            new_points[end] = smoothed_points[end]
        end

fill!(new_points, (P <: NTuple{2, Float64} ? (-9999.0, -9999.0) : UnitSphericalPoint(-9999.0, -9999.0, -9999.0)))

        for i in eachindex(smoothed_points)[begin:end-1]
            p1 = smoothed_points[i]
            p2 = smoothed_points[i+1]
            _add_smoothed_points!(manifold, new_points, p1, p2, n)
            n += 2
        end

        if isring # Close it
            new_points[end] = new_points[begin]
        end

        smoothed_points = new_points
    end

    return smoothed_points
end

function _add_smoothed_points!(::Planar, new_points, p1, p2, n)
    q_x = 0.75 * GI.x(p1) + 0.25 * GI.x(p2)
    q_y = 0.75 * GI.y(p1) + 0.25 * GI.y(p2)
    r_x = 0.25 * GI.x(p1) + 0.75 * GI.x(p2)
    r_y = 0.25 * GI.y(p1) + 0.75 * GI.y(p2)

    new_points[n] = (q_x, q_y)
    new_points[n+1] = (r_x, r_y)
end

For spherical points, we can simply slerp.

function _add_smoothed_points!(::Spherical, new_points, p1, p2, n)
    q = slerp(p1, p2, 0.25)
    r = slerp(p1, p2, 0.75)

    new_points[n] = q
    new_points[n+1] = r
end

---

This page was generated using Literate.jl.